
【題目】已知函數f(x)是定義在R上的偶函數,且當x>0時,函數f(x)的解析式為![]() .
.
(1)求當x<0時函數f(x)的解析式;
(2)用定義證明f(x)在(0,+∞)上的是減函數.
科目:高中數學 來源: 題型:
【題目】如圖在四面體ABCD中,若截面PQMN是正方形,則在下列命題中正確的有 .(填上所有正確命題的序號)
①AC⊥BD
②AC=BD
③AC∥截面PQMN
④異面直線PM與BD所成的角為45°.
查看答案和解析>>
科目:高中數學 來源: 題型:
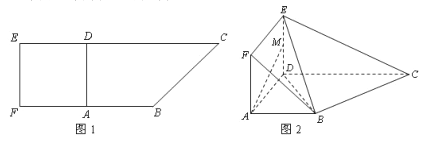
【題目】如圖 1,在直角梯形![]() 中,
中, ![]() ,且
,且![]() .現以
.現以![]() 為一邊向形外作正方形
為一邊向形外作正方形![]() ,然后沿邊
,然后沿邊![]() 將正方形
將正方形![]() 翻折,使
翻折,使![]() 平面與平面
平面與平面![]() 垂直,
垂直, ![]() 為
為![]() 的中點,如圖 2.
的中點,如圖 2.
(1)求證: ![]() 平面
平面![]() ;
;
(2)求證: ![]() 平面
平面![]() ;
;
(3)求點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C:x2+y2+2x﹣4y+3=0.
(1)若圓C的切線在x軸和y軸上的截距相等,求此切線的方程;
(2)從圓C外一點P(x1 , y1)向該圓引一條切線,切點為M,O為坐標原點,且有|PM|=|PO|,求使得|PM|取得最小值的點P的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
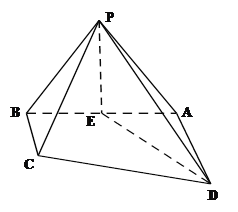
【題目】如圖,四棱錐P—ABCD中,底面ABCD是直角梯形,∠DAB=90°,AD//BC,且BC⊥PB,△PAB是等邊三角形,DA=AB=2,BC=![]() AD,E是線段AB的中點.
AD,E是線段AB的中點.
(I)求證:PE⊥CD;
(II)求PC與平面PDE所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 經過
經過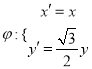 變換后得曲線
變換后得曲線![]() .
.
(1)求![]() 的方程;
的方程;
(2)若![]() 為曲線
為曲線![]() 上兩點,
上兩點, ![]() 為坐標原點,直線
為坐標原點,直線![]() 的斜率分別為
的斜率分別為![]() 且
且![]() ,求直線
,求直線![]() 被圓
被圓![]() 截得弦長的最大值及此時直線
截得弦長的最大值及此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() ,g(x)=ax﹣3.
,g(x)=ax﹣3.
(1)當a=l時,確定函數h(x)=f(x)﹣g(x)在(0,+∞)上的單調性;
(2)若對任意x∈[0,4],總存在x0∈[﹣2,2],使得g(x0)=f(x)成立,求 實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com