
【題目】如圖,有一邊長為6的正方形鐵片,在鐵片的四角各截去一個邊長為x的小正方形后,沿圖中虛線部分折起,做成一個無蓋方盒. 
(1)試用x表示方盒的容積V(x),并寫出x的范圍;
(2)求方盒容積V(x)的最大值及相應x的值.
【答案】
(1)解:由題意,無蓋方盒底面是邊長為6﹣2x的正方形,高為x,
從而有:V(x)=x(6﹣2x)2=4x3﹣24x2+36x,
其中,x滿足: ![]() ,∴0<x<3
,∴0<x<3
(2)解:由(1)知:V(x)=4x3﹣24x2+36x,x∈(0,3),
V′(x)=12x2﹣48x+36=12(x﹣1)(x﹣3),
若0<x<1,則V′(x)>0;若1<x<3,則V′(x)<0,
∴V(x)在(0,1)上單調遞增,在(1,3)上單調遞減,
∴V(x)在x=1處取得極大值,也是最大值,
∴V(x)max=V(1)=16,
故方盒容積V(x)的最大值為16,相應x的值為1
【解析】(1)求出方盒的容積V(x),根據邊長大于0,求出x的范圍即可;(2)求出v(x)的導數,根據函數的單調性求出v(x)的最大值以及相應x的值即可.


科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱 ![]() 中,點E,F分別是棱CC1 , BB1上的點,點M是線段AC上的動點,EC=2FB=2,若MB∥平面AEF,試判斷點M的位置.
中,點E,F分別是棱CC1 , BB1上的點,點M是線段AC上的動點,EC=2FB=2,若MB∥平面AEF,試判斷點M的位置.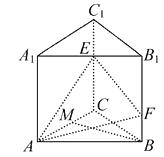
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】求傾斜角為直線y= ![]() +1的傾斜角的一半,且分別滿足下列條件的直線方程:(1)
+1的傾斜角的一半,且分別滿足下列條件的直線方程:(1)
【答案】解:∵直線l1:y= ![]() +1的斜率k1=
+1的斜率k1= ![]() ,
,
∴直線l1的傾斜角為120°,∴所求直線的傾斜角為60°,斜率k= ![]() .
.
∵過點(-4,1),∴直線方程為y-1= ![]() (x+4)
(x+4)
(1)經過點(-4,1)
(2)在y軸上的截距為-10.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知p:|x﹣a|<3(a為常數);q:代數式 ![]() 有意義.
有意義.
(1)若a=1,求使“p∧q”為真命題的實數x的取值范圍;
(2)若p是q成立的充分不必要條件,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=alnx+(x﹣c)|x﹣c|,a<0,c>0 (Ⅰ)當 ![]() 時,求函數f(x)的單調區間;
時,求函數f(x)的單調區間;
(Ⅱ)設函數f(x)的圖象在點P(x1 , f(x1)),Q(x2 , f(x2))兩處的切線分別為l1 , l2 . 若 ![]() ,且l1⊥l2 , 求實數c的最小值.
,且l1⊥l2 , 求實數c的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某產品出廠前需要依次通過三道嚴格的審核程序,三道審核程序通過的概率依次為 ![]() ,
, ![]() ,
, ![]() ,每道程序是相互獨立的,且一旦審核不通過就停止審核,該產品只有三道程序都通過才能出廠銷售 (Ⅰ)求審核過程中只通過兩道程序的概率;
,每道程序是相互獨立的,且一旦審核不通過就停止審核,該產品只有三道程序都通過才能出廠銷售 (Ⅰ)求審核過程中只通過兩道程序的概率;
(Ⅱ)現有3件該產品進入審核,記這3件產品可以出廠銷售的件數為X,求X的分布列及數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com