
【題目】若數(shù)列{an}滿足an+1=an+( ![]() )n , a1=1,則an= .
)n , a1=1,則an= .
【答案】2﹣ ![]() (n∈N*)
(n∈N*)
【解析】解:由已知可得,an+1﹣an=( ![]() )n , 所以有:a2﹣a1=(
)n , 所以有:a2﹣a1=( ![]() )1 , a3﹣a2=(
)1 , a3﹣a2=( ![]() )2 , …,an﹣an﹣1=(
)2 , …,an﹣an﹣1=( ![]() )n﹣1(n≥2), 上述n﹣1個(gè)式子累加可得:an﹣a1=(
)n﹣1(n≥2), 上述n﹣1個(gè)式子累加可得:an﹣a1=( ![]() )1+(
)1+( ![]() )2+…+(
)2+…+( ![]() )n﹣1=
)n﹣1= 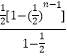 =
= ![]() (n≥2),
(n≥2),
所以得,an=a1+ ![]() =2﹣
=2﹣ ![]() (n≥2),
(n≥2),
因?yàn)楫?dāng)n=1時(shí)上式也成立,因此有an=2﹣ ![]() (n∈N*)
(n∈N*)
答:2﹣ ![]() (n∈N*)
(n∈N*)
【考點(diǎn)精析】掌握數(shù)列的通項(xiàng)公式是解答本題的根本,需要知道如果數(shù)列an的第n項(xiàng)與n之間的關(guān)系可以用一個(gè)公式表示,那么這個(gè)公式就叫這個(gè)數(shù)列的通項(xiàng)公式.


 課課練江蘇系列答案
課課練江蘇系列答案 名牌中學(xué)課時(shí)作業(yè)系列答案
名牌中學(xué)課時(shí)作業(yè)系列答案 明天教育課時(shí)特訓(xùn)系列答案
明天教育課時(shí)特訓(xùn)系列答案 浙江新課程三維目標(biāo)測評(píng)課時(shí)特訓(xùn)系列答案
浙江新課程三維目標(biāo)測評(píng)課時(shí)特訓(xùn)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】我國南宋時(shí)期著名的數(shù)學(xué)家秦九韶在其著作《數(shù)書九章》中,提出了已知三角形三邊長求三角形的面積的公式,與著名的海倫公式完全等價(jià),由此可以看出我國古代已具有很高的數(shù)學(xué)水平,其求法是:“以小斜冪并大斜冪減中斜冪,余半之,自乘于上.以小斜冪乘大斜冪減上,余四約之,為實(shí).一為從隔,開平方得積.”若把以上這段文字寫成公式,即 ,其中a、b、c分別為
,其中a、b、c分別為![]() 內(nèi)角A、B、C的對(duì)邊.若
內(nèi)角A、B、C的對(duì)邊.若![]() ,
,![]() ,則
,則![]() 面積S的最大值為
面積S的最大值為
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線l經(jīng)過直線2x+y-5=0與x-2y=0的交點(diǎn)P.
(1)若直線l平行于直線l1:4x-y+1=0,求l的方程;
(2)若直線l垂直于直線l1:4x-y+1=0,求l的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系中,點(diǎn)![]() 是直線
是直線![]() 上的動(dòng)點(diǎn),定點(diǎn)
上的動(dòng)點(diǎn),定點(diǎn)![]() 點(diǎn)
點(diǎn)![]() 為
為![]() 的中點(diǎn),動(dòng)點(diǎn)
的中點(diǎn),動(dòng)點(diǎn)![]() 滿足
滿足![]() .
.
(1)求點(diǎn)![]() 的軌跡
的軌跡![]() 的方程
的方程
(2)過點(diǎn)![]() 的直線交軌跡
的直線交軌跡![]() 于
于![]() 兩點(diǎn),
兩點(diǎn),![]() 為
為![]() 上任意一點(diǎn),直線
上任意一點(diǎn),直線![]() 交
交![]() 于
于![]() 兩點(diǎn),以
兩點(diǎn),以![]() 為直徑的圓是否過
為直徑的圓是否過![]() 軸上的定點(diǎn)? 若過定點(diǎn),求出定點(diǎn)的坐標(biāo);若不過定點(diǎn),說明理由。
軸上的定點(diǎn)? 若過定點(diǎn),求出定點(diǎn)的坐標(biāo);若不過定點(diǎn),說明理由。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】高斯是德國著名的數(shù)學(xué)家,近代數(shù)學(xué)奠基者之一,享有“數(shù)學(xué)王子”的稱號(hào),他和阿基米德、牛頓并列為世界三大數(shù)學(xué)家,用其名字命名的“高斯函數(shù)”為:設(shè)x∈R,用[x]表示不超過x的最大整數(shù),則y=[x]稱為高斯函數(shù),例如:[-3.5]=-4,[2.1]=2,已知函數(shù)![]() ,則關(guān)于函數(shù)g(x)=[f(x)]的敘述正確的是( )
,則關(guān)于函數(shù)g(x)=[f(x)]的敘述正確的是( )
A. ![]() 是偶函數(shù)B.
是偶函數(shù)B. ![]() 是奇函數(shù)
是奇函數(shù)
C. ![]() 的值域是
的值域是![]() 0,
0,![]() D.
D. ![]() 的值域是
的值域是![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
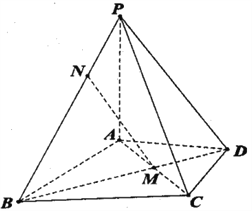
【題目】如圖,在四棱錐![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 是
是![]() 與
與![]() 的交點(diǎn),點(diǎn)
的交點(diǎn),點(diǎn)![]() 在線段
在線段![]() 上,且
上,且![]() .
.
(1)證明:![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某企業(yè)2017年的純利潤為500萬元,因設(shè)備老化等原因,企業(yè)的生產(chǎn)能力逐年下降,若不能進(jìn)行技術(shù)改造,預(yù)測從2018年起每年比上一年純利潤減少20萬元,2018年初該企業(yè)一次性投入資金600萬元進(jìn)行技術(shù)改造,預(yù)測在未扣除技術(shù)改造資金的情況下,第![]() 年(以2018年為第一年)的利潤為
年(以2018年為第一年)的利潤為![]() 萬元(
萬元(![]() 為正整數(shù)).
為正整數(shù)).
(1)設(shè)從今年起的前![]() 年,若該企業(yè)不進(jìn)行技術(shù)改造的累計(jì)純利潤為
年,若該企業(yè)不進(jìn)行技術(shù)改造的累計(jì)純利潤為![]() 萬元,進(jìn)行技術(shù)改造后的累計(jì)純利潤為
萬元,進(jìn)行技術(shù)改造后的累計(jì)純利潤為![]() 萬元(須扣除技術(shù)改造資金),求
萬元(須扣除技術(shù)改造資金),求![]() ,
,![]() 的表達(dá)式;
的表達(dá)式;
(2)依上述預(yù)測,從2018年起該企業(yè)至少經(jīng)過多少年,進(jìn)行技術(shù)改造后的累計(jì)利潤超過不進(jìn)行技術(shù)改造的累計(jì)純利潤?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,直線
中,直線![]() 的參數(shù)方程是
的參數(shù)方程是 (
(![]() 為參數(shù)),以
為參數(shù)),以![]() 為極點(diǎn),
為極點(diǎn), ![]() 軸的正半軸為極軸,建立極坐標(biāo)系,曲線
軸的正半軸為極軸,建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,且直線
,且直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點(diǎn).
兩點(diǎn).
(Ⅰ)求直線![]() 的普通方程及曲線
的普通方程及曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(Ⅱ)把直線![]() 與
與![]() 軸的交點(diǎn)記為
軸的交點(diǎn)記為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com