
【題目】已知函數![]() 的部分圖像如圖所示,
的部分圖像如圖所示,![]() 兩點之間的距離為10,且
兩點之間的距離為10,且![]() ,若將函數
,若將函數![]() 的圖像向右平移
的圖像向右平移![]() 個單位長度后所得函數圖像關于
個單位長度后所得函數圖像關于![]() 軸對稱,則
軸對稱,則![]() 的最小值為( )
的最小值為( )
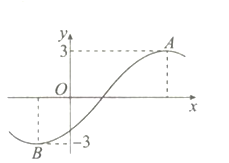
A.1B.2C.3D.4
 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案科目:高中數學 來源: 題型:
【題目】天津市某學校組織教師進行“學習強國”知識競賽,規則為:每位參賽教師都要回答3個問題,且對這三個問題回答正確與否相互之間互不影響,若每答對1個問題,得1分;答錯,得0分,最后按照得分多少排出名次,并分一、二、三等獎分別給予獎勵.已知對給出的3個問題,教師甲答對的概率分別為![]() ,
,![]() ,p.若教師甲恰好答對3個問題的概率是
,p.若教師甲恰好答對3個問題的概率是![]() ,則
,則![]() ________;在前述條件下,設隨機變量X表示教師甲答對題目的個數,則X的數學期望為________.
________;在前述條件下,設隨機變量X表示教師甲答對題目的個數,則X的數學期望為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某籃球隊甲、乙兩名運動員練習罰球,每人練習10組,每組罰球40個.命中個數的莖葉圖如圖,則下面結論中錯誤的一個是( )

A. 甲的極差是29 B. 甲的中位數是24
C. 甲罰球命中率比乙高 D. 乙的眾數是21
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校高中三個年級共有4000人,為了了解各年級學周末在家的學習情況,現通過分層抽樣的方法獲得相關數據如下(單位:小時),其中高一學生周末的平均學習時間記為![]() .
.
高一:14 15 15.5 16.5 17 17 18 19
高二:15 16 16 16 17 17 18.5
高三:16 17 18 21.5 24
(1)求每個年級的學生人數;
(2)從高三被抽查的同學中隨機抽取2人,求2人學習時間均超過![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 企業為了監控某種零件的一條流水生產線的產品質量,檢驗員從該生產線上隨機抽取100個零件,測量其尺寸
企業為了監控某種零件的一條流水生產線的產品質量,檢驗員從該生產線上隨機抽取100個零件,測量其尺寸![]() (單位:
(單位:![]() )并經過統計分析,得到這100個零件的平均尺寸為10,標準差為0.5.企業規定:若
)并經過統計分析,得到這100個零件的平均尺寸為10,標準差為0.5.企業規定:若![]() ,該零件為一等品,企業獲利20元;若
,該零件為一等品,企業獲利20元;若![]() 且
且![]() ,該零件為二等品,企業獲利10元;否則,該零件為不合格品,企業損失40元.
,該零件為二等品,企業獲利10元;否則,該零件為不合格品,企業損失40元.
(1)在某一時刻內,依次下線10個零件,如果其中出現了不合格品,就認為這條生產線在這一天的生產過程可能出現了異常情況,需對當天的生產過程進行檢查若這10個零件的尺寸分別為9.6,10.5,9.8,10.1,10.7,9.4,10.9,9.5,10,10.9,則從這一天抽檢的結果看,是否需要對當天的生產過程進行檢查?
(2)將樣本的估計近似地看作總體的估計通過檢驗發現,該零件的尺寸![]() 服從正態分布
服從正態分布![]() .其中近似為樣本平均數,
.其中近似為樣本平均數,![]() 近似為樣本方差
近似為樣本方差![]() .
.
(i)從下線的零件中隨機抽取20件,設其中為合格品的個數為![]() ,求
,求![]() 的數學期望(結果保留整數)
的數學期望(結果保留整數)
(ii)試估計生產10000個零件所獲得的利潤.
附:若隨機變量![]() 服從正態分布
服從正態分布![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() ,
, ![]() ,函數
,函數![]() ,
, ![]() .
.
(Ⅰ)若![]() 與
與![]() 有公共點
有公共點![]() ,且在
,且在![]() 點處切線相同,求該切線方程;
點處切線相同,求該切線方程;
(Ⅱ)若函數![]() 有極值但無零點,求實數
有極值但無零點,求實數![]() 的取值范圍;
的取值范圍;
(Ⅲ)當![]() ,
, ![]() 時,求
時,求![]() 在區間
在區間![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數![]() 對任意的
對任意的![]() ,均有
,均有![]() ,則稱函數
,則稱函數![]() 具有性質
具有性質![]() .
.
(1)判斷下面兩個函數是否具有性質![]() ,并說明理由.①
,并說明理由.①![]() ;②
;②![]() .
.
(2)若函數![]() 具有性質
具有性質![]() ,且
,且![]() ,求證:對任意
,求證:對任意![]() 有
有![]() ;
;
(3)在(2)的條件下,是否對任意![]() 均有
均有![]() .若成立給出證明,若不成立給出反例.
.若成立給出證明,若不成立給出反例.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】第18屆國際籃聯籃球世界杯(世界男子籃球錦標賽更名為籃球世界杯后的第二屆世界杯)于2019年8月31日至9月15日在中國的北京、廣州、南京、上海、武漢、深圳、佛山、東莞八座城市舉行.中國隊12名球員在第一場和第二場得分的莖葉圖如圖所示,則下列說法錯誤的是( )
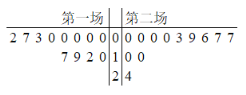
A.第一場得分的中位數為![]() B.第二場得分的平均數為
B.第二場得分的平均數為![]()
C.第一場得分的極差大于第二場得分的極差D.第一場與第二場得分的眾數相等
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com