
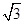 ,則該三角形的面積的最大值為 ▲ .
,則該三角形的面積的最大值為 ▲ . 

科目:高中數學 來源:不詳 題型:解答題
 是底部
是底部 不可到達的一個塔型建筑物,
不可到達的一個塔型建筑物, 為塔的最高點.現需在對岸測出塔高
為塔的最高點.現需在對岸測出塔高 ,甲、乙兩同學各提出了一種測量方法.
,甲、乙兩同學各提出了一種測量方法. 在同一水平面內的一條基線
在同一水平面內的一條基線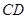 ,使
,使 三點不在同一
三點不在同一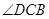 及
及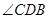 的大小(分別用
的大小(分別用 表示測得的數據)以及
表示測得的數據)以及 間的距離(用
間的距離(用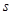 表示測得的數據),另外需在點
表示測得的數據),另外需在點 測得塔頂
測得塔頂 的仰角(用
的仰角(用 表示測量的數據),就可以求得塔高
表示測量的數據),就可以求得塔高 .
. ,使
,使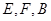 三點在同一條直線上.在
三點在同一條直線上.在 處分別測得塔頂
處分別測得塔頂 的仰角(分別用
的仰角(分別用 表示測得的數據)以及
表示測得的數據)以及 間的距離(用
間的距離(用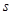 表示測得的數據),就可以求得塔高
表示測得的數據),就可以求得塔高 .
. 按逆時針方向標注,
按逆時針方向標注,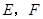 按從左到右的方向標注;③求塔高
按從左到右的方向標注;③求塔高 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com