
【題目】已知函數(shù)![]()
![]() .
.
(1)求函數(shù)![]() 的極小值;
的極小值;
(2)求證:當(dāng)![]() 時(shí),
時(shí),![]() .
.
【答案】(1)見(jiàn)解析(2)見(jiàn)解析
【解析】
(1)由題意可得![]() 分類(lèi)討論函數(shù)的極小值即可.
分類(lèi)討論函數(shù)的極小值即可.
(2)令![]() ,原問(wèn)題等價(jià)于
,原問(wèn)題等價(jià)于![]() ,即證
,即證![]() .據(jù)此分類(lèi)討論
.據(jù)此分類(lèi)討論![]() ,
,![]() 和
和![]() 三種情況即可證得題中的結(jié)論.
三種情況即可證得題中的結(jié)論.
(1)![]()
當(dāng)![]() 時(shí),即
時(shí),即![]() 時(shí),
時(shí),![]() ,函數(shù)
,函數(shù)![]() 在
在![]() 上單調(diào)遞增,無(wú)極小值;
上單調(diào)遞增,無(wú)極小值;
當(dāng)![]() 時(shí),即
時(shí),即![]() 時(shí),
時(shí),![]() ,函數(shù)
,函數(shù)![]() 在
在![]() 上單調(diào)遞減;
上單調(diào)遞減;
![]() ,函數(shù)
,函數(shù)![]() 在
在![]() 上單調(diào)遞增;
上單調(diào)遞增;
![]() ,
,
綜上所述,當(dāng)![]() 時(shí),
時(shí),![]() 無(wú)極小值;當(dāng)
無(wú)極小值;當(dāng)![]() 時(shí),
時(shí),![]()
(2)令![]()
當(dāng)![]() 時(shí),要證:
時(shí),要證:![]() ,即證
,即證![]() ,即證
,即證![]() ,
,
要證![]() ,即證
,即證![]() .
.
①當(dāng)![]() 時(shí),
時(shí),
令![]() ,
,![]() ,所以
,所以![]() 在
在![]() 單調(diào)遞增,
單調(diào)遞增,
故![]() ,即
,即![]() .
.
![]() ,
,
令![]() ,
,![]() ,
,
當(dāng)![]() ,
,![]() 在
在![]() 單調(diào)遞減;
單調(diào)遞減;![]() ,
,![]() 在
在![]() 單調(diào)遞增,故
單調(diào)遞增,故![]() ,即
,即![]() .當(dāng)且僅當(dāng)
.當(dāng)且僅當(dāng)![]() 時(shí)取等號(hào)
時(shí)取等號(hào)
又![]() ,
,![]()
由![]() 、
、![]() 可知
可知![]()
所以當(dāng)![]() 時(shí),
時(shí),![]()
②當(dāng)![]() 時(shí),即證
時(shí),即證![]() .令
.令![]() ,
,![]() ,
,![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增,
上單調(diào)遞增,![]() ,故
,故![]()
③當(dāng)![]() 時(shí),當(dāng)
時(shí),當(dāng)![]() 時(shí),
時(shí),![]() ,由②知
,由②知![]() ,而
,而![]() ,
,
故![]() ;
;
當(dāng)![]() 時(shí),
時(shí),![]() ,由②知
,由②知![]() ,故
,故![]() ;
;
所以,當(dāng)![]() 時(shí),
時(shí),![]() .
.
綜上①②③可知,當(dāng)![]() 時(shí),
時(shí),![]() .
.


 永乾教育寒假作業(yè)快樂(lè)假期延邊人民出版社系列答案
永乾教育寒假作業(yè)快樂(lè)假期延邊人民出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知a為實(shí)數(shù),函數(shù)f(x)=aln x+x2-4x.
(1)是否存在實(shí)數(shù)a,使得f(x)在x=1處取得極值?證明你的結(jié)論;
(2)設(shè)g(x)=(a-2)x,若x0∈![]() ,使得f(x0)≤g(x0)成立,求實(shí)數(shù)a的取值范圍.
,使得f(x0)≤g(x0)成立,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】線段AB為圓![]() 的一條直徑,其端點(diǎn)A,B在拋物線
的一條直徑,其端點(diǎn)A,B在拋物線![]() 上,且A,B兩點(diǎn)到拋物線C焦點(diǎn)的距離之和為11.
上,且A,B兩點(diǎn)到拋物線C焦點(diǎn)的距離之和為11.
(1)求拋物線C的方程及直徑AB所在的直線方程;
(2)過(guò)M點(diǎn)的直線l交拋物線C于P,Q兩點(diǎn),拋物線C在P,Q處的切線相交于N點(diǎn),求![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,三棱柱![]() 中,
中,![]() 分別為棱
分別為棱![]() 的中點(diǎn).
的中點(diǎn).
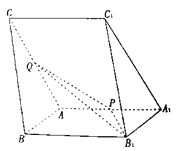
(1)在![]() 上確定點(diǎn)M,使
上確定點(diǎn)M,使![]() 平面
平面![]() ,并說(shuō)明理由。
,并說(shuō)明理由。
(2)若側(cè)面![]() 側(cè)面
側(cè)面![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)點(diǎn)![]() 為拋物線
為拋物線![]() 上的動(dòng)點(diǎn),
上的動(dòng)點(diǎn),![]() 是拋物線的焦點(diǎn),當(dāng)
是拋物線的焦點(diǎn),當(dāng)![]() 時(shí),
時(shí),![]() .
.
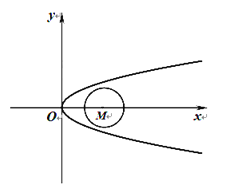
(1)求拋物線![]() 的方程;
的方程;
(2)過(guò)點(diǎn)![]() 作圓
作圓![]() :
:![]() 的切線
的切線![]() ,
,![]() ,分別交拋物線
,分別交拋物線![]() 于點(diǎn)
于點(diǎn)![]() .當(dāng)
.當(dāng)![]() 時(shí),求
時(shí),求![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在五面體![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ..
..
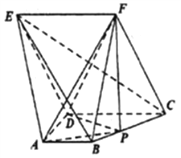
(1)證明:直線![]() 平面
平面![]() ;
;
(2)已知![]() 為棱
為棱![]() 上的點(diǎn),試確定
上的點(diǎn),試確定![]() 點(diǎn)位置,使二面角
點(diǎn)位置,使二面角![]() 的大小為
的大小為![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖兩個(gè)同心球,球心均為點(diǎn)![]() ,其中大球與小球的表面積之比為3:1,線段
,其中大球與小球的表面積之比為3:1,線段![]() 與
與![]() 是夾在兩個(gè)球體之間的內(nèi)弦,其中
是夾在兩個(gè)球體之間的內(nèi)弦,其中![]() 兩點(diǎn)在小球上,
兩點(diǎn)在小球上,![]() 兩點(diǎn)在大球上,兩內(nèi)弦均不穿過(guò)小球內(nèi)部.當(dāng)四面體
兩點(diǎn)在大球上,兩內(nèi)弦均不穿過(guò)小球內(nèi)部.當(dāng)四面體![]() 的體積達(dá)到最大值時(shí),此時(shí)異面直線
的體積達(dá)到最大值時(shí),此時(shí)異面直線![]() 與
與![]() 的夾角為
的夾角為![]() ,則
,則![]() ( )
( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】金秋九月,丹桂飄香,某高校迎來(lái)了一大批優(yōu)秀的學(xué)生,新生接待其實(shí)也是和社會(huì)溝通的一個(gè)平臺(tái).校團(tuán)委、學(xué)生會(huì)從在校學(xué)生中隨機(jī)抽取了160名學(xué)生,對(duì)是否愿意投入到新生接待工作進(jìn)行了問(wèn)卷調(diào)查,統(tǒng)計(jì)數(shù)據(jù)如下:
愿意 | 不愿意 | |
男生 | 60 | 20 |
女生 | 40 | 40 |
(1)通過(guò)估算,試判斷男、女哪種性別的學(xué)生愿意投入到新生接待工作的概率更大.
(2)能否有99%的把握認(rèn)為,愿意參加新生接待工作與性別有關(guān)?
附: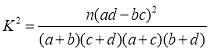 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知拋物線![]() 的焦點(diǎn)為
的焦點(diǎn)為![]() .
.
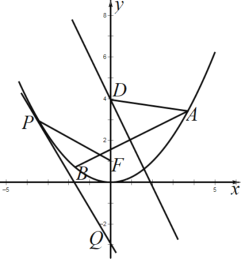
![]() 若點(diǎn)
若點(diǎn)![]() 為拋物線上異于原點(diǎn)的任一點(diǎn),過(guò)點(diǎn)
為拋物線上異于原點(diǎn)的任一點(diǎn),過(guò)點(diǎn)![]() 作拋物線的切線交
作拋物線的切線交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,證明:
,證明:![]() .
.
![]()
![]() ,
,![]() 是拋物線上兩點(diǎn),線段
是拋物線上兩點(diǎn),線段![]() 的垂直平分線交
的垂直平分線交![]() 軸于點(diǎn)
軸于點(diǎn)![]() (
(![]() 不與
不與![]() 軸平行),且
軸平行),且![]() .過(guò)
.過(guò)![]() 軸上一點(diǎn)
軸上一點(diǎn)![]() 作直線
作直線![]() 軸,且
軸,且![]() 被以
被以![]() 為直徑的圓截得的弦長(zhǎng)為定值,求
為直徑的圓截得的弦長(zhǎng)為定值,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com