Question

【題目】若函數(shù)在區(qū)間上的值域為，則稱區(qū)間為函數(shù)的一個“倒值區(qū)間”.定義在上的奇函數(shù)，當時，

（Ⅰ）求函數(shù)的解析式；

（Ⅱ）求函數(shù)在上的“倒值區(qū)間”；

（Ⅲ）記函數(shù)在整個定義域內(nèi)的“倒值區(qū)間”為，設(shè)，則是否存在實數(shù)，使得函數(shù)的圖像與函數(shù)的圖像有兩個不同的交點？若存在，求出的值；若不存在，試說明理由．

Answer 1

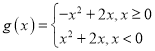【答案】（Ⅰ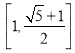）； （Ⅱ）；（Ⅲ）

【解析】

（Ⅰ）當，利用函數(shù)奇偶性可知，代入求得時的解析式，從而得到分段函數(shù)解析式；（Ⅱ）設(shè)，利用單調(diào)性和“倒值區(qū)間”的定義可得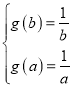，解方程求得結(jié)果；（Ⅲ）當時，，不滿足在上的值域，可知在上的“倒值區(qū)間”為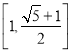，同理可得在上的“倒值區(qū)間”；根據(jù)解析式可得到交點位置，根據(jù)交點位置可得關(guān)于的方程，利用函數(shù)值域可求得的范圍；通過兩段范圍可確定的取值.

（Ⅰ）當時，

為奇函數(shù)

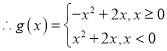
（Ⅱ）設(shè)，由（Ⅰ）知，在上單調(diào)遞減

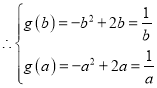，整理得：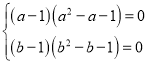

解得：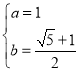

函數(shù)在上的“倒值區(qū)間”為：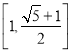

（Ⅲ）由（Ⅱ）知，函數(shù)在上的“倒值區(qū)間”為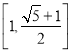

當?shù)怪祬^(qū)間時，

而函數(shù)在上的值域為

函數(shù)在上不存在倒值區(qū)間

即：函數(shù)在上的“倒值區(qū)間”為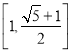

當時，同理可求得的倒值區(qū)間為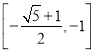

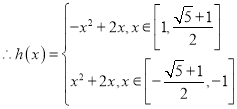
若函數(shù)的圖像與的圖像有兩個不同的交點，則兩個交點分別在第一、三象限

當交點在第一象限時，方程

即：在區(qū)間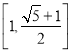內(nèi)恰有一個解

當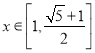，單調(diào)遞減且

當交點在第三象限時，方程

即：在區(qū)間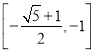內(nèi)恰有一個解

綜上可得：