
【題目】(1)某校夏令營有3名男同學A、B、C和3名女同學X、Y、Z,其年級情況如下表:
一年級 | 二年級 | 三年級 | |
男同學 | A | B | C |
女同學 | X | Y | Z |
現從這6名同學中隨機選出2人參加知識競賽(每人被選到的可能性相同).
①用表中字母列舉出所有可能的結果;
②設M為事件“選出的2人來自不同年級且恰有1名男同學和1名女同學”,求事件M發生的概率.
(2)節日前夕,小李在家門前的樹上掛了兩串彩燈.這兩串彩燈的第一次閃亮相互獨立,且都在通電后的4秒內任一時刻等可能發生,然后每串彩燈以4秒為間隔閃亮.那么這兩串彩燈同時通電后,它們第一次閃亮的時刻相差不超過2秒的概率是多少?
【答案】(1)①詳見解析②![]() (2)
(2)![]()
【解析】
(1)①用表中字母一一列舉出所有可能的結果,共15個;
②用列舉法求出事件![]() 包含的結果有6個,符合古典概型的特征,由此求得事件
包含的結果有6個,符合古典概型的特征,由此求得事件![]() 發生的概率;
發生的概率;
(2)符合幾何概型的特征,設第一串彩燈亮的時刻為![]() ,第二串彩燈亮的時刻為
,第二串彩燈亮的時刻為![]() ,用不等式表示出條件,畫出圖象,根據面積之比求出概率.
,用不等式表示出條件,畫出圖象,根據面積之比求出概率.
解:(1)①從6名同學中隨機選出2人參加知識競賽的所有可能結果為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共15種;
,共15種;
②選出的2人來自不同年級且恰有1名男同學和1名女同學的所有可能結果為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共6種,
,共6種,
因此,事件M發生的概率![]() ;
;
(2)設第一串彩燈亮的時刻為![]() ,第二串彩燈亮的時刻為
,第二串彩燈亮的時刻為![]() ,則
,則![]() ,
,
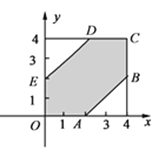
要使兩串彩燈亮的時刻相差不超過2秒,則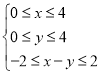 ,
,
如圖,不等式組![]() 所表示的圖形面積為16,
所表示的圖形面積為16,
不等式組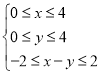 所表示的六邊形的面積為
所表示的六邊形的面積為![]() ,
,
由幾何概型的公式可得![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】隨著我國經濟的飛速發展,人民生活水平得到很大提高,汽車已經進入千千萬萬的家庭.大部分的車主在購買汽車時,會在轎車或者![]() 中作出選擇,為了研究某地區哪種車型更受歡迎以及汽車一年內的行駛里程,某汽車銷售經理作出如下統計:
中作出選擇,為了研究某地區哪種車型更受歡迎以及汽車一年內的行駛里程,某汽車銷售經理作出如下統計:
購買了轎車(輛) | 購買了 | |
|
|
|
|
|
|
(1)根據表,是否有![]() 的把握認為年齡與購買的汽車車型有關?
的把握認為年齡與購買的汽車車型有關?
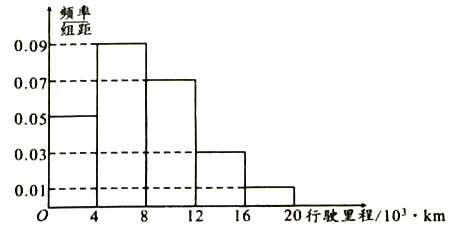
(2)圖給出的是![]() 名車主上一年汽車的行駛里程,求這
名車主上一年汽車的行駛里程,求這![]() 名車主上一年汽車的平均行駛里程(同一組中的數據用該組區間的中點值作代表);
名車主上一年汽車的平均行駛里程(同一組中的數據用該組區間的中點值作代表);
(3)用分層抽樣的方法從![]() 歲以上車主中抽取
歲以上車主中抽取![]() 人,再從這
人,再從這![]() 人中隨機抽取
人中隨機抽取![]() 人贈送免費保養券,求這
人贈送免費保養券,求這![]() 人中至少有
人中至少有![]() 輛轎車的概率。
輛轎車的概率。
附:![]() ,
,![]()
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 漢字聽寫大會
漢字聽寫大會![]() 不斷創收視新高,為了避免“書寫危機”,弘揚傳統文化,某市大約10萬名市民進行了漢字聽寫測試
不斷創收視新高,為了避免“書寫危機”,弘揚傳統文化,某市大約10萬名市民進行了漢字聽寫測試![]() 現從某社區居民中隨機抽取50名市民的聽寫測試情況,發現被測試市民正確書寫漢字的個數全部在160到184之間,將測試結果按如下方式分成六組:第1組
現從某社區居民中隨機抽取50名市民的聽寫測試情況,發現被測試市民正確書寫漢字的個數全部在160到184之間,將測試結果按如下方式分成六組:第1組![]() ,第2組
,第2組![]() ,
,![]() ,第6組
,第6組![]() ,如圖是按上述分組方法得到的頻率分布直方圖.
,如圖是按上述分組方法得到的頻率分布直方圖.

![]() 若電視臺記者要從抽取的市民中選1人進行采訪,求被采訪人恰好在第2組或第6組的概率;
若電視臺記者要從抽取的市民中選1人進行采訪,求被采訪人恰好在第2組或第6組的概率;
![]() 試估計該市市民正確書寫漢字的個數的平均數與中位數;
試估計該市市民正確書寫漢字的個數的平均數與中位數;
![]() 已知第4組市民中有3名男性,組織方要從第4組中隨機抽取2名市民組成弘揚傳統文化宣傳隊,求至少有1名女性市民的概率.
已知第4組市民中有3名男性,組織方要從第4組中隨機抽取2名市民組成弘揚傳統文化宣傳隊,求至少有1名女性市民的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在多面體ABD﹣A1B1C1D1中四邊形A1B1C1D1,ADD1A1.ABB1A1均為正方形.點M是BD的中點.點H在線段C1M上,且A1H與平面ABD所成角的正弦值為![]() .
.
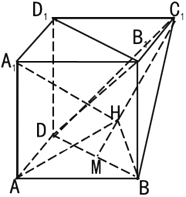
(Ⅰ)證明:B1D1∥平面BC1D:
(Ⅱ)求二面角A﹣A1H﹣B的的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設P是橢圓![]() 上一點,M,N分別是兩圓(x+4)2+y2=1和(x-4)2+y2=1上的點,則|PM|+|PN|的最小值、最大值分別為 ( )
上一點,M,N分別是兩圓(x+4)2+y2=1和(x-4)2+y2=1上的點,則|PM|+|PN|的最小值、最大值分別為 ( )
A. 9,12 B. 8,11 C. 10,12 D. 8,12
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設P是橢圓![]() 上一點,M,N分別是兩圓(x+4)2+y2=1和(x-4)2+y2=1上的點,則|PM|+|PN|的最小值、最大值分別為 ( )
上一點,M,N分別是兩圓(x+4)2+y2=1和(x-4)2+y2=1上的點,則|PM|+|PN|的最小值、最大值分別為 ( )
A. 9,12 B. 8,11 C. 10,12 D. 8,12
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正三角形![]() 的邊長為3,
的邊長為3,![]() 分別是
分別是![]() 邊上的點,滿足
邊上的點,滿足![]() (如圖1).將
(如圖1).將![]() 折起到
折起到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() ,連接
,連接![]() (如圖2).
(如圖2).
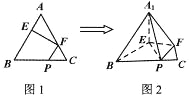
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的前
的前![]() 項和為
項和為![]() .數列
.數列![]() 滿足
滿足![]() ,
,![]() .
.
(1)若![]() ,且
,且![]() ,求正整數
,求正整數![]() 的值;
的值;
(2)若數列![]() ,
,![]() 均是等差數列,求
均是等差數列,求![]() 的取值范圍;
的取值范圍;
(3)若數列![]() 是等比數列,公比為
是等比數列,公比為![]() ,且
,且![]() ,是否存在正整數
,是否存在正整數![]() ,使
,使![]() ,
,![]() ,
,![]() 成等差數列,若存在,求出一個
成等差數列,若存在,求出一個![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠對一批產品進行了抽樣檢測.右圖是根據抽樣檢測后的產品凈重(單位:克)數據繪制的頻率分布直方圖,其中產品凈重的范圍是[96,106],樣本數據分組為[96,98),[98,100),[100,102),[102,104),[104,106],已知樣本中產品凈重小于100克的個數是36,則樣本中凈重大于或等于98克并且小于104克的產品的個數是( ).
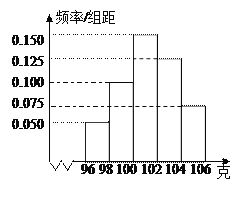
A. 90B. 75C. 60D. 45
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com