【題目】已知一圓經過點A（2，﹣3）和B（﹣2，﹣5），且圓心C在直線l：x﹣2y﹣3=0上，求此圓的方程．
【答案】解：（解法一）因為圓經過點A（2，﹣3），B（﹣2，﹣5），所以線段AB的中點D的坐標為（0，﹣4）， 又 
，所以線段AB的垂直平分線的方程是y=﹣2x﹣4．
聯立方程組 
，解得 
．
所以，圓心坐標為C（﹣1，﹣2），半徑r=|CA|= 
，
所以，此圓的標準方程是（x+1）2+（y+2）2=10．
（解法二）解：設圓的標準方程為（x﹣a）2+（y﹣b）2=r2 ，
由題意可得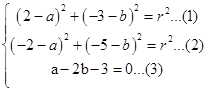 
，
由（2）﹣（1）可得2a+b+4=0，∵ 
，∴ 
，
綜上所述，圓的標準方程為（x+1）2+（y+2）2=10
【解析】（解法一）：先求出線段AB的中垂線的方程，再把它和圓心C在直線l的方程聯立方程組，求得圓心坐標，可得半徑，從而求得此圓的方程． （解法二）：待定系數法，設圓的標準方程為（x﹣a）2+（y﹣b）2=r2 ， 由條件聯立方程組求出a、b、r的值，從而求得此圓的方程．
【考點精析】根據題目的已知條件，利用圓的一般方程的相關知識可以得到問題的答案，需要掌握圓的一般方程的特點：(1)①x2和y2的系數相同，不等于0．②沒有xy這樣的二次項；(2)圓的一般方程中有三個特定的系數D、E、F，因之只要求出這三個系數，圓的方程就確定了；(3)、與圓的標準方程相比較，它是一種特殊的二元二次方程，代數特征明顯，圓的標準方程則指出了圓心坐標與半徑大小，幾何特征較明顯．
科目：高中數學 來源： 題型：
【題目】某校為評估新教改對教學的影響，挑選了水平相當的兩個平行班進行對比試驗。甲班采用創新教法，乙班仍采用傳統教法，一段時間后進行水平測試，成績結果全部落在
區間內（滿分100分），并繪制頻率分布直方圖如右圖，兩個班人數均為60人，成績80分及以上為優良。
根據以上信息填好下列
聯表，并判斷出有多大的把握認為學生成績優良與班級有關？
（2）以班級分層抽樣,抽取成績優良的5人參加座談，現從5人中隨機選3人來作書面發言，求發言人至少有2人來自甲班的概率。
(以下臨界值及公式僅供參考
, 
)
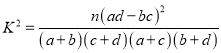查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知f（x）= 
（x≠0，a＞0）是奇函數，且當x＞0時，f（x）有最小值2 
．
（1）求f（x）的表達式；
（2）設數列{an}滿足a1=2，2an+1=f（an）﹣an（n∈N*）．令bn= 
，求證bn+1=bn2；
（3）求數列{bn}的通項公式．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知直線l過點P（1，1），并與直線l1：x﹣y+3=0和l2：2x+y﹣6=0分別交于點A、B，若線段AB被點P平分． 求：
（1）直線l的方程；
（2）以O為圓心且被l截得的弦長為 
的圓的方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知以點A（﹣1，2）為圓心的圓與直線m：x+2y+7=0相切，過點B（﹣2，0）的動直線l與圓A相交于M、N兩點
（1）求圓A的方程．
（2）當|MN|=2 
時，求直線l方程．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
