【題目】如圖，在三棱柱
中，側面
是菱形，
，
是棱
的中點，
，
在線段
上，且
.
（1）證明：
面
；
（2）若
，面
面，求二面角
的余弦值．
【答案】（1）詳見解析；（2）
.
【解析】
（1）連接
交
于點
，連接
，利用三角形相似證明
，然后證明
面
．
（2）過
作
于
，以為原點，
，
，
分別為
軸，
軸，
軸的正方向建立空間直角坐標，
不妨設
，求出面
的一個法向量，面
的一個法向量，然后利用空間向量的數量積求解即可．
解：（1）連接交于點，連接．
因為
，所以
，又因為
，所以
，所以，
又
面，
面，所以面.
（2）過作于，因為
，所以是線段
的中點．
因為面
面
，面
面
，所以
面．連接
，
因為
是等邊三角形，是線段的中點，所以
.
如圖以為原點，，，分別為軸，軸，軸的正方向建立空間直角坐標，
不妨設，則
，
，
，
，
，
由
，得
，
的中點
，
，
.
設面的一個法向量為
，則
，即
，
得方程的一組解為
，即
.
面的一個法向量為
，則
，
所以二面角
的余弦值為.
快樂5加2金卷系列答案科目：高中數學 來源： 題型：
【題目】某大學開學期間，該大學附近一家快餐店招聘外賣騎手，該快餐店提供了兩種日工資結算方案：方案
規定每日底薪100元，外賣業務每完成一單提成2元；方案
規定每日底薪150元，外賣業務的前54單沒有提成，從第55單開始，每完成一單提成5元.該快餐店記錄了每天騎手的人均業務量，現隨機抽取100天的數據，將樣本數據分為
七組，整理得到如圖所示的頻率分布直方圖.
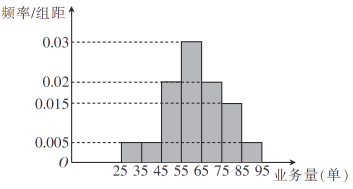
（1）隨機選取一天，估計這一天該快餐店的騎手的人均日外賣業務量不少于65單的概率；
（2）從以往統計數據看，新聘騎手選擇日工資方案的概率為
，選擇方案的概率為
.若甲、乙、丙、丁四名騎手分別到該快餐店應聘，四人選擇日工資方案相互獨立，求至少有兩名騎手選擇方案的概率，
（3）若僅從人日均收入的角度考慮，請你為新聘騎手做出日工資方案的選擇，并說明理由.（同組中的每個數據用該組區間的中點值代替）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】生男生女都一樣，女兒也是傳后人.由于某些地區仍然存在封建傳統思想，頭胎的男女情況可能會影響生二孩的意愿，現隨機抽取某地200戶家庭進行調查統計.這200戶家庭中，頭胎為女孩的頻率為0.5，生二孩的頻率為0.525，其中頭胎生女孩且生二孩的家庭數為60.
（1）完成下列
列聯表，并判斷能否有95%的把握認為是否生二孩與頭胎的男女情況有關；
生二孩 | 不生二孩 | 合計 | |
頭胎為女孩 | 60 | ||
頭胎為男孩 | |||
合計 | 200 |
（2）在抽取的200戶家庭的樣本中，按照分層抽樣的方法在生二孩的家庭中抽取了7戶，進一步了解情況，在抽取的7戶中再隨機抽取4戶，求抽到的頭胎是女孩的家庭戶數
的分布列及數學期望.
附：
| 0.15 | 0.05 | 0.01 | 0.001 |
| 2.072 | 3.841 | 6.635 | 10.828 |
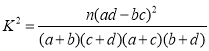（其中
）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】生男生女都一樣，女兒也是傳后人.由于某些地區仍然存在封建傳統思想，頭胎的男女情況可能會影響生二孩的意愿，現隨機抽取某地200戶家庭進行調查統計.這200戶家庭中，頭胎為女孩的頻率為0.5，生二孩的頻率為0.525，其中頭胎生女孩且生二孩的家庭數為60.
（1）完成下列
列聯表，并判斷能否有95%的把握認為是否生二孩與頭胎的男女情況有關；
生二孩 | 不生二孩 | 合計 | |
頭胎為女孩 | 60 | ||
頭胎為男孩 | |||
合計 | 200 |
（2）在抽取的200戶家庭的樣本中，按照分層抽樣的方法在生二孩的家庭中抽取了7戶，進一步了解情況，在抽取的7戶中再隨機抽取4戶，求抽到的頭胎是女孩的家庭戶數
的分布列及數學期望.
附：
| 0.15 | 0.05 | 0.01 | 0.001 |
| 2.072 | 3.841 | 6.635 | 10.828 |
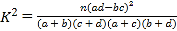（其中
）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，曲線
過點
，其參數方程為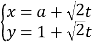
（
為參數， 
），以
為極點， 
軸非負半軸為極軸，建立極坐標系，曲線
的極坐標方程為
.
（1）求曲線
的普通方程和曲線
的直角坐標方程；
（2）求已知曲線
和曲線
交于
兩點，且
，求實數
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的中心為原點
，焦點為
，離心率為
，不與坐標軸垂直的直線
與橢圓
交于
，
兩點.
（1）若
為線段
的中點，求直線的方程.
（2）若點
是直線
上一點，點
在橢圓上，且滿足
，設直線
與直線
的斜率分別為
，
，問
是否為定值？若是，請求出的值；若不是，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系中
中，曲線
的參數方程為
（
為參數，
）.以坐標原點為極點，
軸正半軸為極軸建立極坐標系，已知直線
的極坐標方程為
.
（1）設
是曲線上的一個動點，當
時，求點到直線的距離的最大值；
（2）若曲線上所有的點均在直線的右下方，求
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
