
【題目】設全集U=R,集合![]() ,B={y|y=2x,x≤1},C={x|2a<x<a+1}.
,B={y|y=2x,x≤1},C={x|2a<x<a+1}.
(1)求A∩UB;
(2)若C(A∪B),求實數a的取值范圍.
【答案】(1)A∩UB={x|﹣2≤x≤0};(2)a≥﹣1.
【解析】
(1)解不等式求出集合A,求值域得出集合B,再求A∩UB;
(2)由C(A∪B),討論C=和C≠時,從而求出實數a的取值范圍.
(1)集合A={x|3x+2+31﹣x≤28}
={x|93x+33﹣x≤28}
={x|9(3x)2﹣283x+3≤0}
={x|![]() 3x≤3}
3x≤3}
={x|﹣2≤x≤1},
B={y|y=2x,x≤1}={y|0<y≤2},
∴UB={x|x≤0或x>2},
∴A∩UB={x|﹣2≤x≤0};
(2)由A∪B={x|﹣2≤x≤2},
∵C(A∪B),
當C=時,滿足題意,可得2a≥a+1,
解得:a≥1;
當C≠時,要使C(A∪B),
則 ,解得﹣1≤a<1;
,解得﹣1≤a<1;
綜上知,實數a的取值范圍是a≥﹣1.


科目:高中數學 來源: 題型:
【題目】某校高三課外興趣小組為了解高三同學高考結束后是否打算觀看2018年足球世界杯比賽的情況,從全校高三年級1500名男生、1000名女生中按分層抽樣的方式抽取125名學生進行問卷調查,情況如下表:
打算觀看 | 不打算觀看 | |
女生 | 20 | b |
男生 | c | 25 |
(1)求出表中數據b,c;
(2)判斷是否有99%的把握認為觀看2018年足球世界杯比賽與性別有關;
(3)為了計算“從10人中選出9人參加比賽”的情況有多少種,我們可以發現它與“從10人中選出1人不參加比賽”的情況有多少種是一致的.現有問題:在打算觀看2018年足球世界杯比賽的同學中有5名男生、2名女生來自高三(5)班,從中推選5人接受校園電視臺采訪,請根據上述方法,求被推選出的5人中恰有四名男生、一名女生的概率.
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
K0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
附: 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一只紅鈴蟲的產卵數y和溫度x有關,現收集了6組觀測數據于下表中,通過散點圖可以看出樣本點分布在一條指數型函數y=![]() 的圖象的周圍.
的圖象的周圍.
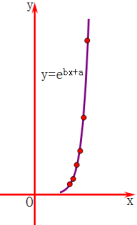
(1)試求出y關于x的上述指數型的回歸曲線方程(結果保留兩位小數);
(2)試用(1)中的回歸曲線方程求相應于點(24,17)的殘差![]() .(結果保留兩位小數)
.(結果保留兩位小數)
溫度x(°C) | 20 | 22 | 24 | 26 | 28 | 30 |
產卵數y(個) | 6 | 9 | 17 | 25 | 44 | 88 |
z=lny | 1.79 | 2.20 | 2.83 | 3.22 | 3.78 | 4.48 |
幾點說明:
①結果中的![]() 都應按題目要求保留兩位小數.但在求
都應按題目要求保留兩位小數.但在求![]() 時請將
時請將![]() 的值多保留一位即用保留三位小數的結果代入.
的值多保留一位即用保留三位小數的結果代入.
②計算過程中可能會用到下面的公式:回歸直線方程的斜率![]() =
= =
= ,截距
,截距![]() .
.
③下面的參考數據可以直接引用:![]() =25,
=25,![]() =31.5,
=31.5,![]() ≈3.05,
≈3.05,![]() =5248,
=5248,![]() ≈476.08,
≈476.08,![]() ,ln18.17≈2.90.
,ln18.17≈2.90.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲乙兩位同學玩游戲,對于給定的實數![]() ,按下列方法操作一次產生一個新的實數:由甲、乙同時各擲一枚均勻的硬幣,如果出現兩個正面朝上或兩個反面朝上,則把
,按下列方法操作一次產生一個新的實數:由甲、乙同時各擲一枚均勻的硬幣,如果出現兩個正面朝上或兩個反面朝上,則把![]() 乘以2后再減去6;如果出現一個正面朝上,一個反面朝上,則把
乘以2后再減去6;如果出現一個正面朝上,一個反面朝上,則把![]() 除以2后再加上6,這樣就可得到一個新的實數
除以2后再加上6,這樣就可得到一個新的實數![]() ,對實數
,對實數![]() 仍按上述方法進行一次操作,又得到一個新的實數
仍按上述方法進行一次操作,又得到一個新的實數![]() ,當
,當![]() 時,甲獲勝,否則乙獲勝,若甲勝的概率為
時,甲獲勝,否則乙獲勝,若甲勝的概率為![]() ,則
,則![]() 的取值范圍是____.
的取值范圍是____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正三棱柱![]() 各條棱的長度均相等,
各條棱的長度均相等,![]() 為
為![]() 的中點,
的中點,![]() 分別是線段
分別是線段![]() 和線段
和線段![]() 上的動點(含端點),且滿足
上的動點(含端點),且滿足![]() ,當
,當![]() 運動時,下列結論中不正確的是( )
運動時,下列結論中不正確的是( )

A. 在![]() 內總存在與平面
內總存在與平面![]() 平行的線段
平行的線段
B. 平面![]() 平面
平面![]()
C. 三棱錐![]() 的體積為定值
的體積為定值
D. ![]() 可能為直角三角形
可能為直角三角形
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com