
【題目】在一次購物抽獎活動中,假設某10張券中有一等獎券1張,可獲價值50元的獎品;有二等獎券3張,每張可獲價值10元的獎品;其余6張沒有獎,某顧客從此10張券中任抽2張,求:
(Ⅰ)該顧客中獎的概率;
(Ⅱ)該顧客獲得的獎品總價值ξ(元)的概率分布列和期望Eξ.
【答案】解:解法一:(Ⅰ)P=1﹣ ![]() =1﹣
=1﹣ ![]() =
= ![]() ,即該顧客中獎的概率為
,即該顧客中獎的概率為 ![]() . (Ⅱ)ξ的所有可能值為:0,10,20,50,60(元).
. (Ⅱ)ξ的所有可能值為:0,10,20,50,60(元).
且P(ξ=0)= ![]() =
= ![]() ,P(ξ=10)=
,P(ξ=10)= ![]() =
= ![]() ,
,
P(ξ=20)= ![]() =
= ![]() ,P(ξ=50)=
,P(ξ=50)= ![]() =
= ![]() ,
,
P(ξ=60)= ![]() =
= ![]()
故ξ有分布列:
ξ | 0 | 10 | 20 | 50 | 60 |
P |
|
|
|
|
|
從而期望Eξ=0× ![]() +10×
+10× ![]() +20×
+20× ![]() +50×
+50× ![]() +60×
+60× ![]() =16.
=16.
解法二:
(Ⅰ)P= 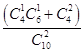 =
= ![]() =
= ![]() ,
,
(Ⅱ)ξ的分布列求法同解法一
由于10張券總價值為80元,即每張的平均獎品價值為8元,從而抽2張的平均獎品價值Eξ=2×8=16(元)
【解析】(1)先求中獎的對立事件“沒中獎”的概率,求“沒中獎”的概率是古典概型.(2)ξ的所有可能值為:0,10,20,50,60,用古典概型分別求概率,列出分布列,再求期望即可.


科目:高中數學 來源: 題型:
【題目】某家庭進行理財投資,根據長期收益率市場調查和預測,投資債券等穩鍵型產品A的收益與投資成正比,其關系如圖1所示;投資股票等風險型產品B的收益與投資的算術平方根成正比,其關系如圖2所示(收益與投資單位:萬元). 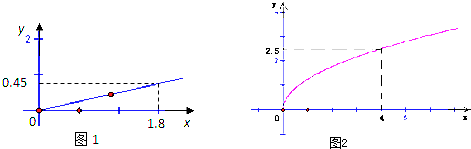
(1)分別將A、B兩種產品的收益表示為投資的函數關系式;
(2)該家庭現有10萬元資金,并全部投資債券等穩鍵型產品A及股票等風險型產品B兩種產品,問:怎樣分配這10萬元投資,才能使投資獲得最大收益,其最大收益為多少萬元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ln (x+1)-![]() -x,a∈R.
-x,a∈R.
(1)當a>0時,求函數f(x)的單調區間;
(2)若存在x>0,使f(x)+x+1<-![]() (a∈Z)成立,求a的最小值.
(a∈Z)成立,求a的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某研究小組為了研究某品牌智能手機在正常使用情況下的電池供電時間,分別從該品牌手機的甲、乙兩種型號中各選取![]() 部進行測試,其結果如下:
部進行測試,其結果如下:
甲種手機供電時間(小時) |
|
|
|
|
|
|
乙種手機供電時間(小時) |
|
|
|
|
|
|
(1)求甲、乙兩種手機供電時間的平均值與方差,并判斷哪種手機電池質量好;
(2)為了進一步研究乙種手機的電池性能,從上述![]() 部乙種手機中隨機抽取
部乙種手機中隨機抽取![]() 部,記所抽
部,記所抽![]() 部手機供電時間不小于
部手機供電時間不小于![]() 小時的個數為
小時的個數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某研究小組為了研究某品牌智能手機在正常使用情況下的電池供電時間,分別從該品牌手機的甲、乙兩種型號中各選取![]() 部進行測試,其結果如下:
部進行測試,其結果如下:
甲種手機供電時間(小時) |
|
|
|
|
|
|
乙種手機供電時間(小時) |
|
|
|
|
|
|
(1)求甲、乙兩種手機供電時間的平均值與方差,并判斷哪種手機電池質量好;
(2)為了進一步研究乙種手機的電池性能,從上述![]() 部乙種手機中隨機抽取
部乙種手機中隨機抽取![]() 部,記所抽
部,記所抽![]() 部手機供電時間不小于
部手機供電時間不小于![]() 小時的個數為
小時的個數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來我國電子商務行業迎來發展的新機遇,與此同時,相關管理部門推出了針對電商商品和服務的評價體系.現從評價系統中選出200次成功交易,并對其評價進行統計,對商品好評率為![]() ,對服務好評率為
,對服務好評率為![]() ,其中對商品和服務都做出好評的交易為80次.
,其中對商品和服務都做出好評的交易為80次.
(1)是否可以在犯錯誤率不超過0.1%的前提下,認為商品好評與服務好評有關?
(2)若針對商品的好評率,采用分層抽樣的方式從這200次交易中取出5次交易,并從中選擇兩次交易進行客戶回訪,求只有一次好評的概率.
注:1.
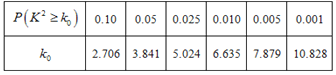
注2. 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】袋子里有編號為![]() 的五個球,某位教師從袋中任取兩個不同的球. 教師把所取兩球編號的和只告訴甲,其乘積只告訴乙,讓甲、乙分別推斷這兩個球的編號.
的五個球,某位教師從袋中任取兩個不同的球. 教師把所取兩球編號的和只告訴甲,其乘積只告訴乙,讓甲、乙分別推斷這兩個球的編號.
甲說:“我無法確定.”
乙說:“我也無法確定.”
甲聽完乙的回答以后,甲又說:“我可以確定了.”
根據以上信息, 你可以推斷出抽取的兩球中
A. 一定有3號球 B. 一定沒有3號球 C. 可能有5號球 D. 可能有6號球
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com