Question

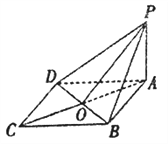
【題目】如圖，矩形，下列結論中不正確的是（ ）

A. B. C. D.

Answer 1

【答案】A

【解析】分析：由PA⊥矩形ABCD，得PA⊥BD，若PD⊥BD，則BD⊥平面PAD，又BA⊥平面PAD，則過平面外一面有兩條直線與平面垂直，不成立，故PD⊥BD不正確．

詳解：∵PA⊥矩形ABCD，

∴PA⊥BD，若PD⊥BD，則BD⊥平面PAD，

又BA⊥平面PAD，則過平面外一面有兩條直線與平面垂直，不成立，

故PD⊥BD不正確，故A不正確；

∵PA⊥矩形ABCD，

∴PA⊥CD，AD⊥CD，

∴CD⊥平面PAD，∴PD⊥CD，故B正確；

∵PA⊥矩形ABCD，

∴由三垂線定理得PB⊥BC，故C正確；

∵PA⊥矩形ABCD，

∴由直線與平面垂直的性質得PA⊥BD，故D正確．

故選：A．