
【題目】如圖,橢圓![]() ,
,![]() 軸被曲線
軸被曲線![]() 截得的線段長等于C1的長半軸長.
截得的線段長等于C1的長半軸長.
(1)求實數b的值;
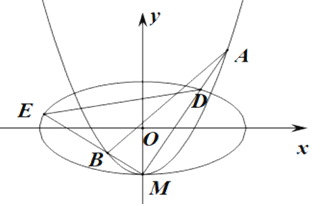
(2)設C2與![]() 軸的交點為M,過坐標原點O的直線
軸的交點為M,過坐標原點O的直線![]() 與C2相交于點A、B,直線MA、MB分別與C1交于點D、E.
與C2相交于點A、B,直線MA、MB分別與C1交于點D、E.
①證明:![]() ;
;
②記△MAB,△MDE的面積分別是![]() 若
若![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)①證明見解析;②
;(2)①證明見解析;②![]() .
.
【解析】
試題(1)由題意直接求得![]() ;(2)①由題意,設直線
;(2)①由題意,設直線![]() 的方程為
的方程為![]() ,聯立方程,利用韋達定理求得
,聯立方程,利用韋達定理求得![]() ,從而
,從而![]() ,即
,即![]() ,故
,故![]() ;②設
;②設![]() 的方程為分別與拋物線的方程聯立,求得點
的方程為分別與拋物線的方程聯立,求得點![]() 的坐標,利用兩點間距離公式求出
的坐標,利用兩點間距離公式求出![]() ,得到
,得到![]() 的表達式,然后把
的表達式,然后把![]() 表示成關于
表示成關于![]() 的函數,進而求出
的函數,進而求出![]() 的取值范圍.
的取值范圍.
試題解析:(1)由題意知:半長軸為![]() ,則有
,則有![]() ,所以
,所以![]() .
.
(2)①由題意知,直線![]() 的斜率存在,設為
的斜率存在,設為![]() ,則直線
,則直線![]() 的方程為
的方程為![]() .
.
由![]() 得
得![]() , 設
, 設![]() ,則
,則![]() 是上述方程的兩個實根,于是
是上述方程的兩個實根,于是![]() .又點
.又點![]() 的坐標為
的坐標為![]() ,所以
,所以![]()
![]()
故![]() ,即
,即![]() ,故
,故![]() .
.
②設![]() 的斜率為
的斜率為![]() ,則
,則![]() 的方程為
的方程為![]() ,由
,由![]() 解得
解得![]() 或
或![]() ,則點
,則點![]() 的坐標為
的坐標為![]() ,又直線
,又直線![]() 的斜率為
的斜率為![]() ,同理可得點
,同理可得點![]() 的坐標為
的坐標為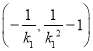 .于是
.于是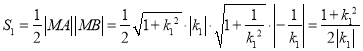
由![]() 得
得![]() ,
,
解得![]() 或
或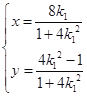 ,則點
,則點![]() 的坐標為
的坐標為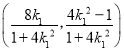 ;
;
又直線![]() 的斜率為
的斜率為![]() ,同理可得點
,同理可得點![]() 的坐標
的坐標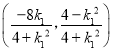 ,
,
于是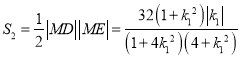
因此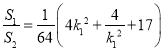 ,又由點
,又由點![]() 的坐標可知,
的坐標可知,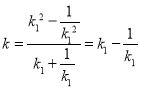 ,平方后代入上式,所以
,平方后代入上式,所以![]() , 故
, 故![]() 的取值范圍為
的取值范圍為![]() .
.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓E: ![]() ,對于任意實數k,下列直線被橢圓E截得的弦長與l:y=kx+1被橢圓E截得的弦長不可能相等的是( )
,對于任意實數k,下列直線被橢圓E截得的弦長與l:y=kx+1被橢圓E截得的弦長不可能相等的是( )
A. kx+y+k=0 B. kx-y-1=0
C. kx+y-k=0 D. kx+y-2=0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】柴靜《穹頂之下》的播出,讓大家對霧霾天氣的危害有了更進一步的認識,對于霧霾天氣的研究也漸漸活躍起來,某研究機構對春節燃放煙花爆竹的天數x與霧霾天數y進行統計分析,得出下表數據.
x | 4 | 5 | 7 | 8 |
y | 2 | 3 | 5 | 6 |
(1)請根據上表提供的數據,用最小二乘法求出y關于x的線性回歸方程![]() ;
;
(2)試根據(1)求出的線性回歸方程,預測燃放煙花爆竹的天數為9的霧霾天數.
(相關公式: )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,圓
,圓![]() .
.
(1)若直線![]() 過點
過點![]() 且到圓心
且到圓心![]() 的距離為
的距離為![]() ,求直線
,求直線![]() 的方程;
的方程;
(2)設過點![]() 的直線
的直線![]() 與圓
與圓![]() 交于
交于![]() 、
、![]() 兩點(
兩點(![]() 的斜率為負),當
的斜率為負),當![]() 時,求以線段
時,求以線段![]() 為直徑的圓的方程.
為直徑的圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在抗擊新型冠狀病毒肺炎期間,為響應政府號召,郴州市某單位組織了志愿者30人,其中男志愿者18人,用分層抽樣的方法從該單位志愿者中抽取5人去參加某社區的防疫幫扶活動.
(1)求從該單位男、女志愿者中各抽取的人數;
(2)從抽取的5名志愿者中任選2名談此活動的感受,求選出的2名志愿者中恰有1名男志愿者的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】故宮博物院五一期間同時舉辦“戲曲文化展”、“明代御窖瓷器展”、“歷代青綠山水畫展”、 “趙孟頫書畫展”四個展覽.某同學決定在五一當天的上、下午各參觀其中的一個,且至少參觀一個畫展,則不同的參觀方案共有
A. 6種 B. 8種 C. 10種 D. 12種
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com