
(本小題滿分12分)已知二次函數(shù) 最大值為
最大值為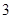 ,且
,且
⑴求 的解析式;
的解析式;
⑵求 在
在 上的最值.
上的最值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12)
為了綠化城市,準(zhǔn)備在如圖所示的區(qū)域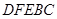 內(nèi)修建一個矩形
內(nèi)修建一個矩形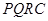 的草坪,并建立如圖平面直角坐標(biāo)系,且
的草坪,并建立如圖平面直角坐標(biāo)系,且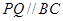 ,
,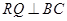 ,另外
,另外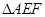 的內(nèi)部有一文物保護(hù)區(qū)不能占用,經(jīng)測量
的內(nèi)部有一文物保護(hù)區(qū)不能占用,經(jīng)測量 ,
,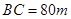 ,
, 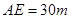 ,
,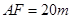 .
.
(1)求直線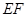 的方程;
的方程;
(2)應(yīng)如何設(shè)計才能使草坪的占地面積最大?并求最大面積。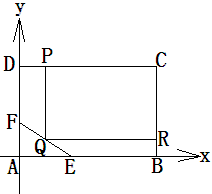
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)已知函數(shù)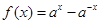 ,
,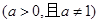 ,
,
(1) 判斷函數(shù) 的奇偶性,并證明;
的奇偶性,并證明;
(2) 判斷 的單調(diào)性,并說明理由。(不需要嚴(yán)格的定義證明,只要說出理由即可)
的單調(diào)性,并說明理由。(不需要嚴(yán)格的定義證明,只要說出理由即可)
(3) 若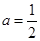 ,方程
,方程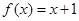 是否有根?如果有根
是否有根?如果有根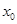 ,請求出一個長度為1的區(qū)間
,請求出一個長度為1的區(qū)間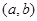 ,使
,使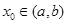 ;如果沒有,請說明理由。(注:區(qū)間
;如果沒有,請說明理由。(注:區(qū)間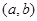 的長度=
的長度=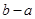 )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)
已知函數(shù)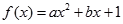 (
(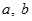 為實數(shù),
為實數(shù),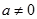 ,
,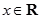 ),若
),若 ,且函數(shù)
,且函數(shù) 的值域為
的值域為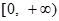 .
.
(1)求 的表達(dá)式;
的表達(dá)式;
(2)當(dāng)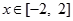 時,
時,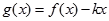 是單調(diào)函數(shù),求實數(shù)
是單調(diào)函數(shù),求實數(shù) 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)如圖所示,某房地產(chǎn)開發(fā)公司計劃在一樓區(qū)內(nèi)建造一個長方形公園ABCD,公園由長方形的休閑區(qū)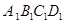 (陰影部分)和環(huán)公園人行道組成.已知休閑區(qū)
(陰影部分)和環(huán)公園人行道組成.已知休閑區(qū)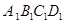 的面積為4000 m 2,人行道的寬分別為4 m和10 m.
的面積為4000 m 2,人行道的寬分別為4 m和10 m.
( I )設(shè)休閑區(qū)的長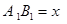 m ,求公園ABCD所占面積
m ,求公園ABCD所占面積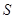 關(guān)于 x 的函數(shù)
關(guān)于 x 的函數(shù)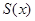 的解析式;
的解析式;
(Ⅱ)要使公園ABCD所占總面積最小,休閑區(qū)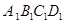 的長和寬該如何設(shè)計?
的長和寬該如何設(shè)計?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)
已知函數(shù)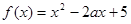 .
.
(1)若 的定義域和值域均是
的定義域和值域均是 ,求實數(shù)
,求實數(shù)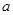 的值;
的值;
(2)若 在區(qū)間
在區(qū)間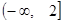 上是減函數(shù),且對任意的
上是減函數(shù),且對任意的
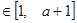 ,總有
,總有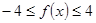 ,求實數(shù)
,求實數(shù)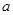 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com