
(理)如圖,平面ADEF⊥平面ABCD,ABCD與ADEF均為矩形,且AB:AD:AF=
|
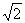 :2:
:2: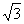 ;P為線段EF上一點,M為AB的中點,若PC與BD所成的角為
;P為線段EF上一點,M為AB的中點,若PC與BD所成的角為
60°.
(1)試確定P點位置;
(2)求二面角P—MC—D的大小的余弦值;
(3)當AB長為多少時,點D到平面PMC的距離等于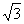 ?
?
(文)設函數 (
( ),其中
),其中 .
.
(Ⅰ)當 時,求曲線
時,求曲線 在點
在點 處的切線方程;
處的切線方程;
(Ⅱ)當 時,求函數
時,求函數 的極大值和極小值;
的極大值和極小值;
(Ⅲ)當 時,證明存在
時,證明存在 ,使得不等式
,使得不等式 對任意的
對任意的 恒成立.
恒成立.
(理)∵AB:AD:AF=2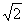 :2:
:2: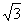
可設AB=2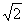 ,AD=2a,AF=
,AD=2a,AF=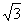 a,并設FP=x建立如圖直角坐標系,則
a,并設FP=x建立如圖直角坐標系,則
A(0,0,0),B(0, 2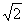 a,0),C(2a, 2
a,0),C(2a, 2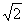 a,0),D(2a,0,0),
a,0),D(2a,0,0),
F(0,0,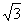 a),E(2a,0,
a),E(2a,0,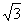 a),M(0,2
a),M(0,2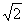 a,0),P(x,0,
a,0),P(x,0,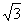 a)…1分
a)…1分
|
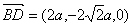
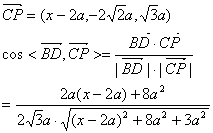
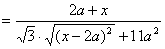 ………………2分
………………2分
∵BD、CP所成角為60°
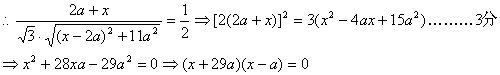
∴x=a,即P點為EF的中點.……………………………………4分
(2)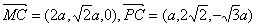
設n=(x,y,z)為平面PMC的一個法向量.
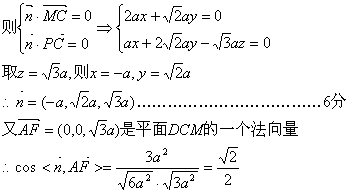
∴二面角P—MC—D的大小的余弦值為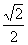 …………………………8分
…………………………8分
(3)設D點到平面PCM的距離為d
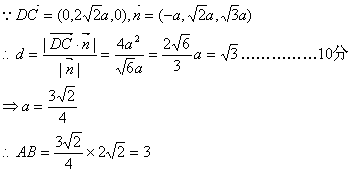
故得當AB=3時,點D到平面PMC的距離等于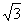 .………………12分
.………………12分
(文)(Ⅰ)解:當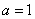 時,
時,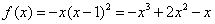 ,得
,得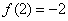 ,且
,且
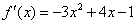 ,
,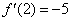 .
.
所以,曲線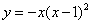 在點
在點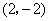 處的切線方程是
處的切線方程是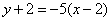 ,整理
,整理
得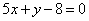 .
.
(Ⅱ)解: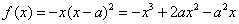
 .
.
令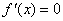 ,解得
,解得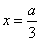 或
或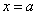 .
.
由于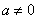 ,以下分兩種情況討論.
,以下分兩種情況討論.
(1)若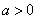 ,當
,當 變化時,
變化時,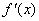 的正負如下表:
的正負如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
因此,函數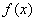 在
在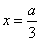 處取得極小值
處取得極小值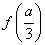 ,且
,且
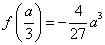 ;
;
函數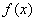 在
在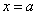 處取得極大值
處取得極大值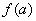 ,且
,且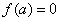 .
.
(2)若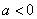 ,當
,當 變化時,
變化時,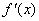 的正負如下表:
的正負如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
因此,函數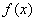 在
在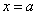 處取得極小值
處取得極小值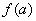 ,且
,且
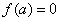 ;
;
函數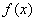 在
在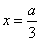 處取得極大值
處取得極大值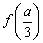 ,且
,且
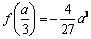 .
.
(Ⅲ)證明:由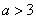 ,得
,得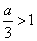 ,當
,當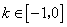 時,
時,
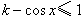 ,
,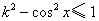 .
.
由(Ⅱ)知,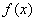 在
在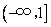 上是減函數,要使
上是減函數,要使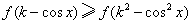 ,
,
只要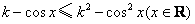
即
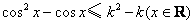 ①
①
設 ,則函數
,則函數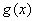 在
在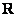 上的最大值為
上的最大值為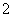 .
.
要使①式恒成立,必須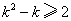 ,即
,即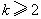 或
或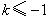 .
.
所以,在區間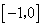 上存在
上存在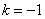 ,使得
,使得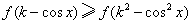 對任意的
對任意的 恒成立.
恒成立.


科目:高中數學 來源: 題型:
 (理)如圖,P為△ABC所在平面外一點,且PA⊥平面ABC,∠ACB=90°,過點A作垂直于PC的截面ADE,截面交PC于點D,交PB于點E.
(理)如圖,P為△ABC所在平面外一點,且PA⊥平面ABC,∠ACB=90°,過點A作垂直于PC的截面ADE,截面交PC于點D,交PB于點E.查看答案和解析>>
科目:高中數學 來源: 題型:
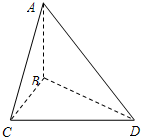 (2013•嘉定區二模)(理)如圖:已知AB⊥平面BCD,BC⊥CD,AD與平面BCD所成的角為30°,且AB=BC=2.
(2013•嘉定區二模)(理)如圖:已知AB⊥平面BCD,BC⊥CD,AD與平面BCD所成的角為30°,且AB=BC=2.查看答案和解析>>
科目:高中數學 來源: 題型:
 (2011•崇明縣二模)(理)如圖,PA⊥平面ABCD,四邊形ABCD是正方形,PA=AD=2,點E、F、G分別為線段PA、PD和CD的中點.
(2011•崇明縣二模)(理)如圖,PA⊥平面ABCD,四邊形ABCD是正方形,PA=AD=2,點E、F、G分別為線段PA、PD和CD的中點.| 4 | 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:
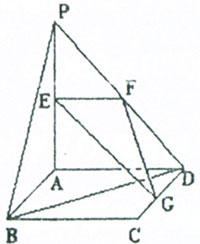
(09年湖北重點中學聯考理)(12分)
如圖,平面PAD⊥平面ABCD,ABCD為正方形,∠PAD=900,且PA=AD=2,E、F、G分別是線段PA、PD、CD的中點。
(1)求證:PB∥平面EFG;
(2)求異面直線EG與BD所成的角;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com