
【題目】已知![]() 是自然數1,2,…,
是自然數1,2,…,![]() 的一個排列,且滿足:對任意
的一個排列,且滿足:對任意![]() ,均有
,均有![]() .
.
(1)若記![]() 為數
為數![]() 在排列中所處位置的序號(如排列
在排列中所處位置的序號(如排列![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ).求證:對每一個滿足題意的排列
).求證:對每一個滿足題意的排列![]() ,均有
,均有![]() 成立.
成立.
(2)試求滿足題意的排列的個數![]() .
.
【答案】(1)見解析(2)![]()
【解析】
(1)證法一:假設結論不成立,則必存在![]() ,
,![]() ,使
,使![]() .
.
不妨設![]() ,
,![]() ,
,![]() .
.
首先證明:對任意整數![]() ,有
,有![]() .
.
若不然,設![]() 中有小于
中有小于![]() 的,設
的,設![]() 為使
為使![]() 的最小
的最小![]() 值,
值,
則由![]() 的最小性知
的最小性知![]() ,
,![]() .
.
故由![]() .得
.得![]() .
.
∴![]() .
.
又因![]() ,故
,故![]() .
.
∴![]() .矛盾.
.矛盾.
故對任意![]() ,
,![]() .
.
∵![]() 是各不相同的自然數,
是各不相同的自然數,
∴![]()
∴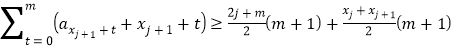
![]()
另一方面,![]() ,
,
∴![]() .
.
于是,![]() ,即
,即![]() ,
,
∴![]() .
.
這與前面矛盾.故結論成立.
證法二:用數學歸納法證明更強的命題:
對任意![]() ,
,![]() .
.
![]() 、2時,易知命題成立.
、2時,易知命題成立.
設![]() 時,命題也成立.
時,命題也成立.
則![]() 時,考慮所有
時,考慮所有![]() 的排列,我們從兩方面求和
的排列,我們從兩方面求和![]() .
.
一方面,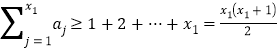 ,
,
∴![]() .
.
另一方面,![]() ,
,
∴![]() .
.
故![]() ,且
,且![]() .
.
因而,![]() ,
,![]() ,…,
,…,![]() ,
,
即當![]() 時,
時,![]() ,
,![]() ,
,![]() .
.
而后![]() 個數的排列,為滿足要求的連續(xù)
個數的排列,為滿足要求的連續(xù)![]() 個數的排列,
個數的排列,
由歸納假設知,![]() 時,也有
時,也有![]() .
.
又易知![]() .這樣的排列僅有一個,即
.這樣的排列僅有一個,即![]() ,同樣也有
,同樣也有![]() .
.
故由數學歸納法知命題成立.
(2)顯然![]() ,
,![]() .假設
.假設![]() ,…,
,…,![]() 均已求出,我們來求
均已求出,我們來求![]() .
.
考慮當![]() 時排列的個數
時排列的個數![]() .
.
由(1)證法二知,此時排列的前![]() 個數是惟一確定的,
個數是惟一確定的,
而后![]() 個連續(xù)自然數的滿足題意的排列方法數為
個連續(xù)自然數的滿足題意的排列方法數為![]() .
.
又對后![]() 數的任一滿足題意的排列,均有
數的任一滿足題意的排列,均有![]() ,
,
故![]() .
.
又![]() ,故
,故![]() .
.
而![]() ,
,
∴![]() .
.
故滿足題意的排列個數![]() .
.


 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,以橢圓
,以橢圓![]() 的左頂點
的左頂點![]() 為圓心作圓
為圓心作圓![]() :
:![]() ,設圓
,設圓![]() 與橢圓
與橢圓![]() 交于點
交于點![]() 與點
與點![]() .
.
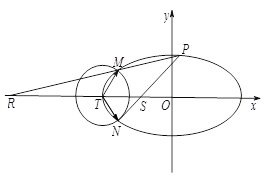
(1)求橢圓![]() 的方程;
的方程;
(2)求![]() 的最小值,并求此時圓
的最小值,并求此時圓![]() 的方程;
的方程;
(3)設點![]() 是橢圓
是橢圓![]() 上異于
上異于![]() ,
,![]() 的任意一點,且直線
的任意一點,且直線![]() 分別與
分別與![]() 軸交于點
軸交于點![]() ,
,![]() 為坐標原點,
為坐標原點,
求證:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】凸![]() 邊形
邊形![]() 玫瑰園的
玫瑰園的![]() 個頂點各栽有1棵紅玫瑰,每兩棵紅玫瑰之間都有一條直小路想通,這些直小路沒有出現(xiàn)“三線共點”的情況——它們把花園分割成許多不重疊的區(qū)域(三角形、四邊形、……),每塊區(qū)域都栽有一棵白玫瑰(或黑玫瑰).
個頂點各栽有1棵紅玫瑰,每兩棵紅玫瑰之間都有一條直小路想通,這些直小路沒有出現(xiàn)“三線共點”的情況——它們把花園分割成許多不重疊的區(qū)域(三角形、四邊形、……),每塊區(qū)域都栽有一棵白玫瑰(或黑玫瑰).
(1)求出玫瑰園里玫瑰總棵樹![]() 的表達式.
的表達式.
(2)花園里能否恰有99棵玫瑰?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2017·全國卷Ⅲ文,18)某超市計劃按月訂購一種酸奶,每天進貨量相同,進貨成本每瓶4元,售價每瓶6元,未售出的酸奶降價處理,以每瓶2元的價格當天全部處理完.根據往年銷售經驗,每天需求量與當天最高氣溫(單位:℃)有關.如果最高氣溫不低于25,需求量為500瓶;如果最高氣溫位于區(qū)間[20,25),需求量為300瓶;如果最高氣溫低于20,需求量為200瓶.為了確定六月份的訂購計劃,統(tǒng)計了前三年六月份各天的最高氣溫數據,得下面的頻數分布表:
最高氣溫 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天數 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高氣溫位于各區(qū)間的頻率估計最高氣溫位于該區(qū)間的概率.
(1)估計六月份這種酸奶一天的需求量不超過300瓶的概率;
(2)設六月份一天銷售這種酸奶的利潤為Y(單位:元).當六月份這種酸奶一天的進貨量為450瓶時,寫出Y的所有可能值,并估計Y大于零的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個圓周上有9個點,以這9個點為頂點作3個三角形.當這3個三角形無公共頂點且邊互不相交時,我們把它稱為一種構圖.滿足這樣條件的構圖共有( )種.
A. 3 B. 6 C. 9 D. 12
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】王府井百貨分店今年春節(jié)期間,消費達到一定標準的顧客可進行一次抽獎活動,隨著抽獎活動的有效開展,參與抽獎活動的人數越來越多,該分店經理對春節(jié)前7天參加抽獎活動的人數進行統(tǒng)計, ![]() 表示第
表示第![]() 天參加抽獎活動的人數,得到統(tǒng)計表格如下:
天參加抽獎活動的人數,得到統(tǒng)計表格如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 5 | 8 | 8 | 10 | 14 | 15 | 17 |
經過進一步統(tǒng)計分析,發(fā)現(xiàn)![]() 與
與![]() 具有線性相關關系.
具有線性相關關系.
(1)請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)判斷變量![]() 與
與![]() 之間是正相關還是負相關;
之間是正相關還是負相關;
(3)若該活動只持續(xù)10天,估計共有多少名顧客參加抽獎.
參與公式:  ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com