
【題目】已知數列{an}滿足a1=1, ![]() ,其中n∈N*.
,其中n∈N*.
(1)設![]() ,求證:數列{bn}是等差數列,并求出{an}的通項公式.
,求證:數列{bn}是等差數列,并求出{an}的通項公式.
(2)設![]() ,數列{cncn+2}的前n項和為Tn,是否存在正整數m,使得
,數列{cncn+2}的前n項和為Tn,是否存在正整數m,使得![]() 對于n∈N*,恒成立?若存在,求出m的最小值;若不存在,請說明.
對于n∈N*,恒成立?若存在,求出m的最小值;若不存在,請說明.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
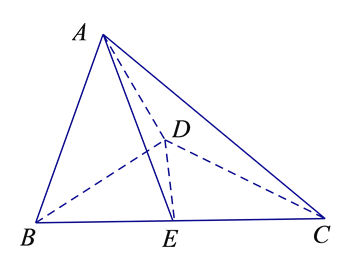
【題目】如圖1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,點E是BC邊的中點,將△ABD沿BD折起,使平面ABD⊥平面BCD,連接AE,AC,DE,得到如圖2所示的幾何體.
(Ⅰ)求證:AB⊥平面ADC;
(Ⅱ)若AD=2,直線CA與平面ABD所成角的正弦值為![]() ,求二面角E-AD-C的余弦值.
,求二面角E-AD-C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
, ![]() 表示兩條不同的直線,
表示兩條不同的直線, ![]() ,
, ![]() ,
, ![]() 表示三個不同的平面,給出下列四個命題:
表示三個不同的平面,給出下列四個命題:
①![]() ,
, ![]() ,
, ![]() ,則
,則![]() ;
;
②![]() ,
, ![]() ,
, ![]() ,則
,則![]() ;
;
③![]() ,
, ![]() ,
, ![]() ,則
,則![]() ;
;
④![]() ,
, ![]() ,
, ![]() ,則
,則![]()
其中正確命題的序號為( )
A. ①② B. ②③ C. ③④ D. ②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知非空集合A={x|2a+1≤x≤3a﹣5},B={x|3≤x≤22},
(1)當a=10時,求A∩B,A∪B;
(2)求能使AB成立的a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=bax(其中a,b為常量,且a>0,a≠1)的圖象經過點A(1,6),B(3,24).
(1)求f(x)的表達式;
(2)設函數g(x)=f(x)﹣2×3x , 求g(x+1)>g(x)時x的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)的定義域為D,若對任意x1 , x2∈D,當x1<x2時,都有f(x1)≤f(x2),則稱函數f(x)在D上為非減函數.設函數f(x)在[0,1]上為非減函數,且滿足以下三個條件:①f(0)=0;② ![]() ;③f(1﹣x)=2﹣f(x).則
;③f(1﹣x)=2﹣f(x).則 ![]() =( )
=( )
A.1
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數y=x2﹣2x的定義域為{0,1,2,3},那么其值域為( )
A.{y|﹣1≤y≤3}
B.{y|0≤y≤3}
C.{0,1,2,3}
D.{﹣1,0,3}
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com