
���}Ŀ����D����ֱ��������![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .
.
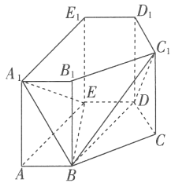
��1���C����![]() ƽ��
ƽ��![]() ��
��
��2����ƽ��![]() �cƽ��
�cƽ��![]() �����J����ǵ�����ֵ.
�����J����ǵ�����ֵ.
���𰸡���1���C��Ҋ(ji��n)������2��![]()
��������
(1)�����}��ɵ�![]() ��
��![]() ���Ķ���
���Ķ���![]() ƽ��
ƽ��![]() ������
������![]() ���ٽY(ji��)��
���ٽY(ji��)��![]() �����C��
�����C��![]() ƽ��
ƽ��![]() ��
��
(2) ��![]() ��ԭ�c(di��n)����
��ԭ�c(di��n)����![]() �ķ���?y��n)?/span>
�ķ���?y��n)?/span>![]() �S��
�S��![]() �S��
�S��![]() �S�������������gֱ������(bi��o)ϵ
�S�������������gֱ������(bi��o)ϵ![]() ��Ȼ��(xi��)�����P(gu��n)�c(di��n)������(bi��o)��������P(gu��n)ƽ��ķ����������딵(sh��)���e��A�ǹ�ʽ����.
��Ȼ��(xi��)�����P(gu��n)�c(di��n)������(bi��o)��������P(gu��n)ƽ��ķ����������딵(sh��)���e��A�ǹ�ʽ����.
(1)�C������?y��n)������?/span>![]() ��ֱ��������
��ֱ��������
����![]() ��
��
��![]() ����
����![]() ��
��
����![]() ƽ��
ƽ��![]() .
.
��?y��n)?/span>![]() ƽ��
ƽ��![]() ������
������![]() .
.
��?y��n)?/span>![]() ��
��![]() ��
��![]() ��
��
����![]() ƽ��
ƽ��![]() .
.

��2���⣺��?y��n)?/span>![]() ������
������![]() ����
����![]() ��ֱ����c(di��n)�ĵ���ֱ�������Σ�
��ֱ����c(di��n)�ĵ���ֱ�������Σ�
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
����![]() ����
����![]() �Ƀɴ�ֱ.
�Ƀɴ�ֱ.
��![]() ��ԭ�c(di��n)����
��ԭ�c(di��n)����![]() �ķ���?y��n)?/span>
�ķ���?y��n)?/span>![]() �S��
�S��![]() �S��
�S��![]() �S��������
�S��������
������D��ʾ�Ŀ��gֱ������(bi��o)ϵ![]() ��
��
�t![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��![]() .
.
�O(sh��)ƽ��![]() �ķ�������
�ķ�������![]() ��
��
�t
��![]() ����ƽ��
����ƽ��![]() ��һ��(g��)��������
��һ��(g��)��������![]() .
.
�O(sh��)ƽ��![]() �ķ�������
�ķ�������![]() ��
��
�t
��![]() ����ƽ��
����ƽ��![]() ��һ��(g��)��������
��һ��(g��)��������![]() .
.
�O(sh��)ƽ��![]() �cƽ��
�cƽ��![]() �����J����Ǟ�
�����J����Ǟ�![]() ��
��
�t .
.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� С�W(xu��)��10��犑�(y��ng)���}ϵ�д�
С�W(xu��)��10��犑�(y��ng)���}ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)f��x��![]() ��cos��+1��cos2x+cos����cosx+1�����������Ă�(g��)�Y(ji��)Փ����f��x����ż����(sh��)����f��x���ڣ�
��cos��+1��cos2x+cos����cosx+1�����������Ă�(g��)�Y(ji��)Փ����f��x����ż����(sh��)����f��x���ڣ�![]() ��
��![]() ���φ��{(di��o)�f�p���ۮ�(d��ng)����[
���φ��{(di��o)�f�p���ۮ�(d��ng)����[![]() ��
��![]() ]�r(sh��)����|f��x��|
]�r(sh��)����|f��x��|![]() ���ܮ�(d��ng)����[
���ܮ�(d��ng)����[![]() ��
��![]() ]�r(sh��)����|f'��x��|
]�r(sh��)����|f'��x��|![]() ���������������}�ľ�̖(h��o)��( )
���������������}�ľ�̖(h��o)��( )
A.�٢�B.�ڢ�C.�٢ۢ�D.�٢�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���O(sh��)![]() ��Ȳ(sh��)��
��Ȳ(sh��)��![]() ��ǰn�(xi��ng)�ͣ�
��ǰn�(xi��ng)�ͣ�![]() �����(xi��ng)�ȱȔ�(sh��)�У���
�����(xi��ng)�ȱȔ�(sh��)�У���![]() ��
��![]() .�ڢ�
.�ڢ�![]() ����
����![]() ����
����![]() �@����(g��)�l�������xһ��(g��)���ش����О��}��
�@����(g��)�l�������xһ��(g��)���ش����О��}��
��1����(sh��)��![]() ��
��![]() ��ͨ�(xi��ng)��ʽ��
��ͨ�(xi��ng)��ʽ��
��2�����![]() ��m��
��m��![]() ������(xi��)��m��n���P(gu��n)ϵʽ
������(xi��)��m��n���P(gu��n)ϵʽ![]() ������
������![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
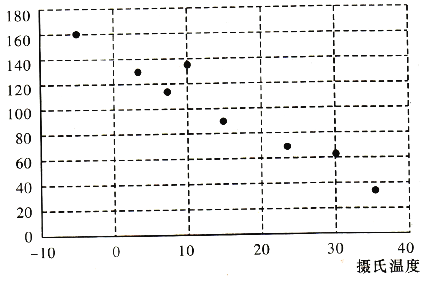
���}Ŀ����һ��(g��)ͬ�W(xu��)���_(k��i)��һ��(g��)С�u(m��i)�����������о���،�(du��)�������N(xi��o)�۵�Ӱ푣���(j��ng)�^(gu��)�y(t��ng)Ӌ(j��)���õ�һ��(g��)�u(m��i)���ğ����(sh��)�c��(d��ng)���ص�ɢ�c(di��n)�D�͌�(du��)�ȱ���
�z�Ϝض� |
|
|
|
|
|
|
|
|
�����(sh��) |
|
|
|
|
|
|
|
|
��1����ɢ�c(di��n)�D���l(f��)�F(xi��n)�����c(di��n)ɢ���ڏ����Ͻǵ����½ǵą^(q��)�����ˣ�����c��(d��ng)�����N(xi��o)�۱���(sh��)֮�g��ؓ(f��)���P(gu��n)�������Խ�ߣ���(d��ng)���u(m��i)��ȥ�ğ����(sh��)Խ�١��y(t��ng)Ӌ(j��)�г������P(gu��n)ϵ��(sh��)![]() ��(l��i)����?j��)ɂ�(g��)׃��֮�g�����P(gu��n)ϵ�ď�(qi��ng)��.�y(t��ng)Ӌ(j��)�W(xu��)�J(r��n)�飬��(du��)��׃��
��(l��i)����?j��)ɂ�(g��)׃��֮�g�����P(gu��n)ϵ�ď�(qi��ng)��.�y(t��ng)Ӌ(j��)�W(xu��)�J(r��n)�飬��(du��)��׃��![]() ��
��![]() �����
�����![]() ����ôؓ(f��)���P(gu��n)��(qi��ng)�����
����ôؓ(f��)���P(gu��n)��(qi��ng)�����![]() ����ô�����P(gu��n)��(qi��ng)�����
����ô�����P(gu��n)��(qi��ng)�����![]() ����ô���P(gu��n)��һ�㣻���
����ô���P(gu��n)��һ�㣻���![]() ����ô���P(gu��n)���^����Ո(q��ng)����(j��)��֪��(sh��)��(j��)���Д�����c��(d��ng)�����N(xi��o)�۱���(sh��)���P(gu��n)�Եď�(qi��ng)��.
����ô���P(gu��n)���^����Ո(q��ng)����(j��)��֪��(sh��)��(j��)���Д�����c��(d��ng)�����N(xi��o)�۱���(sh��)���P(gu��n)�Եď�(qi��ng)��.
��2����i��Ո(q��ng)����(j��)��֪��(sh��)��(j��)�������c��(d��ng)�����N(xi��o)�۱���(sh��)�ľ��Իؚw���̣�
��ii��ӛ![]() �鲻���^(gu��)
�鲻���^(gu��)![]() ���������(sh��)����
���������(sh��)����![]() ��
��![]() .��(du��)�ڣ�i��������ľ��Իؚw����
.��(du��)�ڣ�i��������ľ��Իؚw����![]() ����
����![]() ҕ�����c��(d��ng)�����N(xi��o)�۱���(sh��)�ĺ���(sh��)�P(gu��n)ϵ.��֪?d��)�?/span>
ҕ�����c��(d��ng)�����N(xi��o)�۱���(sh��)�ĺ���(sh��)�P(gu��n)ϵ.��֪?d��)�?/span>![]() �c��(d��ng)����ÿ�����N(xi��o)������(r��n)
�c��(d��ng)����ÿ�����N(xi��o)������(r��n)![]() ���P(gu��n)ϵ��
���P(gu��n)ϵ��![]()
![]() ����λ��Ԫ����Ո(q��ng)��(w��n)��(d��ng)���
����λ��Ԫ����Ո(q��ng)��(w��n)��(d��ng)���![]() ����ٕr(sh��)����(d��ng)��ğ���N(xi��o)������(r��n)���~���
����ٕr(sh��)����(d��ng)��ğ���N(xi��o)������(r��n)���~���
��������ʽ��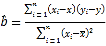 ��
��![]() ��
��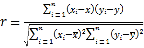
��������(sh��)��(j��)��![]() ��
��![]() ��
��![]()
![]() .
.
![]() ��
��![]() ��
��![]() ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��
![]() ��(d��ng)
��(d��ng)![]() �r(sh��)����(sh��)
�r(sh��)����(sh��)![]() ���{(di��o)���^(q��)�g��
���{(di��o)���^(q��)�g��
![]() ������(sh��)
������(sh��)![]() ��
��![]() ����������(sh��)����(sh��)��(sh��)a��ȡֵ������
����������(sh��)����(sh��)��(sh��)a��ȡֵ������
![]() ��
��![]() ���Ҍ�(du��)����
���Ҍ�(du��)����![]() ��
��![]() ��
��![]() ������
������![]() ����(sh��)��(sh��)a����Сֵ��
����(sh��)��(sh��)a����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() ��(d��o)����(sh��).
��(d��o)����(sh��).
����(d��ng)![]() �r(sh��)����(du��)�������
�r(sh��)����(du��)�������![]() ����
����![]() ����Сֵ��
����Сֵ��
����������![]() ��ʹ
��ʹ![]() ����
����![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�A![]() ��
��![]() ���c(di��n)
���c(di��n)![]() ���c(di��n)
���c(di��n)![]() �LjA
�LjA![]() ������һ�c(di��n)������
������һ�c(di��n)������![]() �Ĵ�ֱƽ�־�������
�Ĵ�ֱƽ�־�������![]() ���c(di��n)
���c(di��n)![]() .
.
��1�����c(di��n)![]() ��܉�E����.
��܉�E����.
��2���O(sh��)�c(di��n)![]() ��
��![]() ��
��![]() ��܉�E�Ϯ�����c(di��n)��������c(di��n)����
��܉�E�Ϯ�����c(di��n)��������c(di��n)����![]() ��ֱ���ĈA�^(gu��)�c(di��n)
��ֱ���ĈA�^(gu��)�c(di��n)![]() .���Cֱ��
.���Cֱ��![]() �^(gu��)���c(di��n)�������ԓ���c(di��n)������(bi��o).
�^(gu��)���c(di��n)�������ԓ���c(di��n)������(bi��o).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���h(hu��n)�����T(m��n)Ҫ��(du��)���е���܇(ch��)ģ���M(j��n)�ЏV���y(c��)ԇ���Դ_��������܇(ch��)?y��n)�̵ĵȼ?j��)���ұ��nj�(du��) 100 �v��܇(ch��)ģ����һ��(g��)���͆�λ��(n��i)��܇(ch��)?y��n)�̣���λ������Ĝy(c��)ԇ�Y(ji��)��.
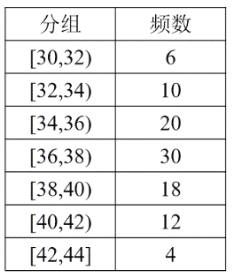
�������������y(c��)ԇ�Y(ji��)�����l�ʷֲ�ֱ���D����ָ������λ��(sh��)������һ�M��
�����÷ӳ�ӵķ�������܇(ch��)?y��n)���څ^(q��)�g[38,40)�c[40,42)����܇(ch��)ģ������ȡ5�v�������@5�v���S�C(j��)��ȡ2�v��������ǡ��һ��(g��)��܇(ch��)ģ����܇(ch��)?y��n)����[40,42)��(n��i)�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��Ӱ����M(f��i)ˮƽ��ԭ��ܶ࣬������Ҫ��һ�(xi��ng)�ǹ��Y����.�о��@�ɂ�(g��)׃�����P(gu��n)ϵ��һ��(g��)������ͨ�^(gu��)�S�C(j��)��ӵķ�������һ��������(n��i)�ռ����{(di��o)���ߵĹ��Y��������������M(f��i)��r.����Ĕ�(sh��)��(j��)��ij�C(j��)��(g��u)�ռ���ijһ���(n��i)�Ϻ������K���㽭�����ա������傀(g��)�^(q��)����ƽ�����Y�c���(zh��n)�������M(f��i)ˮƽ����λ���f(w��n)Ԫ��.
�^(q��) | �Ϻ� | ���K | �㽭 | ���� | ���� |
��ƽ�����Y | 9.8 | 6.9 | 6.4 | 6.2 | 5.6 |
���(zh��n)�������M(f��i)ˮƽ | 6.6 | 4.6 | 4.4 | 3.9 | 3.8 |
��1�����ý��K���㽭����������(g��)�^(q��)����ƽ�����Y�����������M(f��i)ˮƽ��������Իؚw����![]() ������
������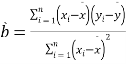
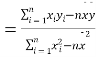 ��
��![]() ��
��
��2�����ɾ��Իؚw���̵õ��Ĺ�Ӌ(j��)��(sh��)��(j��)�c���x���ęz�(y��n)��(sh��)��(j��)���`��������^(gu��)1�f(w��n)���t�J(r��n)��õ��ľ��Իؚw�����ǿɿ��ģ�ԇ��(w��n)���õľ��Իؚw�����Ƿ�ɿ�����![]() �ĽY(ji��)�������λС��(sh��)��
�ĽY(ji��)�������λС��(sh��)��
��������(sh��)��(j��)��![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com