
【題目】如圖,已知矩形![]() ,
, ![]() ,
, ![]() ,點
,點![]() 為矩形內一點,且
為矩形內一點,且![]() ,設
,設![]() .
.
(1)當![]() 時,求
時,求![]() 的值;
的值;
(2)求![]() 的最大值.
的最大值.

【答案】(1)0;(2)2.
【解析】
(1)以A為坐標原點建立直角坐標系,分別求得A,B,C,D,P的坐標,運用向量數量積的坐標表示,計算可得結果;
(2)設P(cosα,sinα),分別求得向量![]() =(2﹣cosα,
=(2﹣cosα,![]() ﹣sinα),
﹣sinα),![]() =(﹣cosα,
=(﹣cosα,![]() ﹣sinα),
﹣sinα),![]() =(cosα,sinα),運用向量數量積的坐標表示,結合輔助角公式和正弦函數的圖象和性質,即可得到所求最大值.
=(cosα,sinα),運用向量數量積的坐標表示,結合輔助角公式和正弦函數的圖象和性質,即可得到所求最大值.
(1)如圖,以A為坐標原點建立直角坐標系,
則A(0,0),B(2,0),C(2,![]() ),D(0,
),D(0,![]() ),
),
P(cos![]() ,sin
,sin![]() ),即(
),即(![]() ,
,![]() ),
),
![]()
![]() =(
=(![]() ,
,![]() )(﹣
)(﹣![]() ,
,![]() )=
)=![]() ×(﹣
×(﹣![]() )+(
)+(![]() )2=0;
)2=0;
(2)設P(cosα,sinα),
則![]() =(2﹣cosα,
=(2﹣cosα,![]() ﹣sinα),
﹣sinα),![]() =(﹣cosα,
=(﹣cosα,![]() ﹣sinα),
﹣sinα),![]() =(cosα,sinα),
=(cosα,sinα),
可得![]() +
+![]() =(2﹣2cosα,2
=(2﹣2cosα,2![]() ﹣2sinα),
﹣2sinα),
則(![]() +
+![]() )
)![]() =2cosα﹣2cos2α+2
=2cosα﹣2cos2α+2![]() sinα﹣2sin2α
sinα﹣2sin2α
=4(![]() sinα+
sinα+![]() cosα)﹣2=4sin(α+
cosα)﹣2=4sin(α+![]() )﹣2,
)﹣2,
當α+![]() =
=![]() ,即α=
,即α=![]() 時,
時,
(![]() )
)![]() 取得最大值4﹣2=2.
取得最大值4﹣2=2.


科目:高中數學 來源: 題型:
【題目】如圖,三棱柱ABC﹣A1B1C1,A1A⊥底面ABC,且△ABC為正三角形,A1A=AB=6,D為AC中點.

(1)求三棱錐C1﹣BCD的體積;
(2)求證:平面BC1D⊥平面ACC1A1;
(3)求證:直線AB1∥平面BC1D.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】
下圖是我國2008年至2014年生活垃圾無害化處理量(單位:億噸)的折線圖
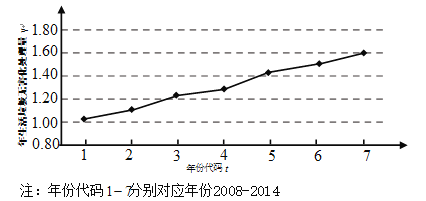
(1)由折線圖看出,可用線性回歸模型擬合![]() 與
與![]() 的關系,請建立
的關系,請建立![]() 關于
關于![]() 的回歸方程(系數精確到0.01);
的回歸方程(系數精確到0.01);
(2)預測2018年我國生活垃圾無害化處理量.
附注:
參考公式:設具有線性相關關系的兩個變量![]() 的一組觀察值為
的一組觀察值為![]() ,
,
則回歸直線方程![]() 的系數為:
的系數為:
 ,
, ![]() .
.
參考數據: ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某設備的使用年數x與所支出的維修總費用y的統計數據如下表:
使用年數x(單位:年) | 2 | 3 | 4 | 5 | 6 |
維修費用y(單位:萬元) | 1.5 | 4.5 | 5.5 | 6.5 | 7.0 |
根據上標可得回歸直線方程為 ![]() =1.3x+
=1.3x+ ![]() ,若該設備維修總費用超過12萬元,據此模型預測該設備最多可使用年.
,若該設備維修總費用超過12萬元,據此模型預測該設備最多可使用年.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中,正確的命題有__________.
①回歸直線![]() 恒過樣本點的中心
恒過樣本點的中心![]() ,且至少過一個樣本點;
,且至少過一個樣本點;
②將一組數據的每個數據都加一個相同的常數后,方差不變;
③用相關指數![]() 來刻面回歸效果;表示預報變量對解釋變量變化的貢獻率,越接近于1,說明模型的擬合效果越好;
來刻面回歸效果;表示預報變量對解釋變量變化的貢獻率,越接近于1,說明模型的擬合效果越好;
④若分類變量![]() 和
和![]() 的隨機變量
的隨機變量![]() 的觀測值
的觀測值![]() 越大,則“
越大,則“![]() 與
與![]() 相關”的可信程度越小;
相關”的可信程度越小;
⑤.對于自變量![]() 和因變量
和因變量![]() ,當
,當![]() 取值一定時,
取值一定時, ![]() 的取值具有一定的隨機性,
的取值具有一定的隨機性, ![]() ,
, ![]() 間的這種非確定關系叫做函數關系;
間的這種非確定關系叫做函數關系;
⑥.殘差圖中殘差點比較均勻的地落在水平的帶狀區域中,說明選用的模型比較合適;
⑦.兩個模型中殘差平方和越小的模型擬合的效果越好.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,曲線C的方程為y=3+ ![]() .
.
(1)寫出曲線C的一個參數方程;
(2)在曲線C上取一點P,過點P作x軸,y軸的垂線,垂足分別為A,B,求矩形OAPB的周長的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() :
: ![]() (
(![]() )的焦點為
)的焦點為![]() ,點
,點![]() 在拋物線
在拋物線![]() 上,且
上,且![]() ,直線
,直線![]() 與拋物線
與拋物線![]() 交于
交于![]() ,
, ![]() 兩點,
兩點, ![]() 為坐標原點.
為坐標原點.
(1)求拋物線![]() 的方程;
的方程;
(2)求![]() 的面積.
的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com