
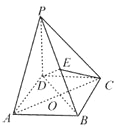
【題目】如圖,在四棱錐![]() 中,
中,![]() 平面
平面![]() ,四邊形
,四邊形![]() 是菱形,
是菱形,![]() ,
,![]() ,且
,且![]() 交于點
交于點![]() ,
,![]() 是
是![]() 上任意一點.
上任意一點.
(1)求證![]() ;
;
(2)已知二面角![]() 的余弦值為
的余弦值為![]() ,若
,若![]() 為
為![]() 的中點,求
的中點,求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)見解析;(2)![]()
【解析】
(1)利用線面垂直的性質得![]() ,利用菱形的性質得
,利用菱形的性質得![]() ,利用線面垂直的判定定理得
,利用線面垂直的判定定理得![]() 平面
平面![]() ,利用線面垂直得到線線垂直,從而得到
,利用線面垂直得到線線垂直,從而得到![]() ;
;
(2)分別以![]() ,
,![]() ,
,![]() 為
為![]() 軸,
軸,![]() 軸,
軸,![]() 軸的正方向建立空間直角坐標系,設
軸的正方向建立空間直角坐標系,設![]() ,用坐標表示點,求得平面
,用坐標表示點,求得平面![]() 的法向量為
的法向量為![]() ,平面
,平面![]() 的法向量為
的法向量為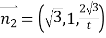 ,根據二面角
,根據二面角![]() 的余弦值為
的余弦值為![]() ,可求出
,可求出![]() ,從而得到點
,從而得到點![]() 的坐標,再利用向量的夾角公式,即可求得
的坐標,再利用向量的夾角公式,即可求得![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
(1)∵![]() 平面
平面![]() ,∴
,∴![]()
又∵四邊形![]() 為菱形,∴
為菱形,∴![]()
又![]() ,∴
,∴![]() 平面
平面![]()
![]() 平面
平面![]() ,∴
,∴![]()
(2)連![]() ,在
,在![]() 中,
中,![]() ,∴
,∴![]() 平面
平面![]()
分別以![]() ,
,![]() ,
,![]() 為
為![]() 軸,
軸,![]() 軸,
軸,![]() 軸的正方向建立空間直角坐標系.
軸的正方向建立空間直角坐標系.
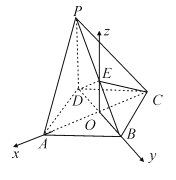
設![]() ,則
,則![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
由(1)知,平面![]() 的一個法向量為
的一個法向量為![]()
設平面![]() 的一個法向量為
的一個法向量為![]() ,則由
,則由
即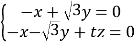 ,令
,令![]() ,則
,則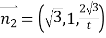
因二面角![]() 的余弦值為
的余弦值為![]() ,
,
∴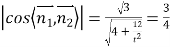 ,∴
,∴![]()
設![]() 與平面
與平面![]() 所成角為
所成角為![]() ,∵
,∵![]() ,
,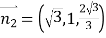 ,
,
∴ .
.


科目:高中數學 來源: 題型:
【題目】已知奇函數f(x)=a![]() (a為常數).
(a為常數).
(1)求a的值;
(2)若函數g(x)=|(2x+1)f(x)|﹣k有2個零點,求實數k的取值范圍;
(3)若x∈[﹣2,﹣1]時,不等式f(x)![]() 恒成立,求實數m的取值范圍.
恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
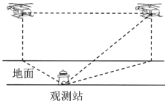
【題目】2019年10月1日,在慶祝新中國成立70周年閱兵中,由我國自主研制的軍用飛機和軍用無人機等參閱航空裝備分秒不差飛越天安門,壯軍威,振民心,令世人矚目.飛行員高超的飛行技術離不開艱苦的訓練和科學的數據分析.一次飛行訓練中,地面觀測站觀測到一架參閱直升飛機以![]() 千米/小時的速度在同一高度向正東飛行,如圖,第一次觀測到該飛機在北偏西
千米/小時的速度在同一高度向正東飛行,如圖,第一次觀測到該飛機在北偏西![]() 的方向上,1分鐘后第二次觀測到該飛機在北偏東
的方向上,1分鐘后第二次觀測到該飛機在北偏東![]() 的方向上,仰角為
的方向上,仰角為![]() ,則直升機飛行的高度為________千米.(結果保留根號)
,則直升機飛行的高度為________千米.(結果保留根號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將曲線![]() 上每個點的橫坐標伸長為原來的
上每個點的橫坐標伸長為原來的![]() 倍(縱坐標不變),得到
倍(縱坐標不變),得到![]() 的圖象,則下列說法正確的是( )
的圖象,則下列說法正確的是( )
A.![]() 的圖象關于直線
的圖象關于直線![]() 對稱
對稱
B.![]() 在
在![]() 上的值域為
上的值域為![]()
C.![]() 的圖象關于點
的圖象關于點![]() 對稱
對稱
D.![]() 的圖象可由
的圖象可由![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度得到
個單位長度得到
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的方程為
的方程為![]() ,橢圓
,橢圓![]() 的離心率正好是雙曲線
的離心率正好是雙曲線![]() 的離心率的倒數,橢圓
的離心率的倒數,橢圓![]() 的短軸長等于拋物線
的短軸長等于拋物線![]() 上一點
上一點![]() 到拋物線焦點
到拋物線焦點![]() 的距離.
的距離.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若直線![]() 與橢圓
與橢圓![]() 的兩個交點為
的兩個交點為![]() ,
,![]() 兩點,已知圓
兩點,已知圓![]() :
:![]() 與
與![]() 軸的交點分別為
軸的交點分別為![]() ,
,![]() (點
(點![]() 在
在![]() 軸的正半軸),且直線
軸的正半軸),且直線![]() 與圓
與圓![]() 相切,求
相切,求![]() 的面積與
的面積與![]() 的面積乘積的最大值.
的面積乘積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術·均輸》中有如下問題:“今有五人分十錢,令上二人所得與下三人等,問各得幾何.”其意思為“已知甲、乙、丙、丁、戊五人分10錢,甲、乙兩人所得與丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差數列,問五人各得多少錢?”(“錢”是古代的一種重量單位).這個問題中,甲所得為( )
A.![]() 錢B.
錢B.![]() 錢C.
錢C.![]() 錢D.
錢D.![]() 錢
錢
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com