【題目】已知函數
.
(1)當
時,討論
的單調性；
(2)設
，當
時,若對任意
,存在
使
,求實數
取值.
【答案】（1）當
時,函數
在
上單調遞減；函數在
上單調遞增；當
時,函數在
上單調遞減；
當
時,函數在上單調遞減；函數在
上單調遞增;函數在
上單調遞減；（2）
．
【解析】分析：（1）先求定義域，再對函數求導，
，
令
，分
，，，
，四種情況考慮h(x)零點情況及正負情況，得函數f(x)的單調區間。
（2）因為
,由于(I)知,在
上的最小值為
，
由題意可知“對任意
,存在
,使
”等價于“
在
上的最小值不大于在上的最小值
”，由一元二次函數的“三點一軸”分類討論求得g(x)的最小值，再求得b范圍。
詳解：(1)定義域
因為
所以
令
(i)當時, 
所以當
時, 
,此時
,函數單調遞增;
當
時, 
,此時
,函數單調遞增
(ii)當
時,由
,
即
,解得
①當時, 
，
恒成立,此時
,函數在上單調遞減;
②當時, 
時, ,此時,函數單調遞減；
時, ,此時,函數單調遞增；
時, ,此時,函數單調遞減；
③當時,由于
時, ,此時,函數單調遞減；
時, ,此時,函數單調遞增；
綜上所述:
當時,函數在
上單調遞減；
函數在上單調遞增；
當時,函數在上單調遞減；
當時,函數在上單調遞減；
函數在
上單調遞增;
函數在
上單調遞減
(2)因為,由于(I)知, 
,當時, ,
函數單調遞減:當
時, ,函數單調遞增,所以在上的最小值為
由于“對任意,存在,使”等價于“在上的最小值不大于在上的最小值”
又
,
,所以
①當
時,因為
,此時與
矛盾
②當
時,因為
,同樣與矛盾
③當
時,因為
，解不等式
可得
綜上, 
的取值范圍是．
科目：高中數學 來源： 題型：
【題目】已知關于
與
有表格中的數據，且與線性相關，由最小二乘法得
.
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
（1）求與的線性回歸方程；
（2）現有第二個線性模型：
，且
.若與（1）的線性模型比較，哪一個線性模型擬合效果比較好，請說明理由
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】中國古代數學名著《九章算術》中“竹九節”問題曰：“今有竹九節，下三節容量四升，上四節容量三升，問中間兩節欲均容各多少？”其意為：“現有一根9節的竹子，自上而下的容積成等差數列，下面3節容量為4升，上面4節容積為3升，問中間2節各多少容積？”則中間2節容積合計________升
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】等比數列{an}的各項均為正數，且2a1＋3a2＝1， 
＝9a2a6.
(1)求數列{an}的通項公式；
(2)設bn＝log3a1＋log3a2＋…＋log3an，求數列
的前n項和．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，直線
，
.
(1)直線
是否過定點？若過定點，求出該定點坐標，若不過定點，請說明理由;
(2)已知點
，若直線上存在點
滿足條件
，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】△ABC的內角A，B，C的對邊分別為a，b，c，已知△ABC的面積為 
．（12分）
（1）求sinBsinC；
（2）若6cosBcosC=1，a=3，求△ABC的周長．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）的定義域為R，且f（2）=2，又函數f（x）的導函數y=f′（x）的圖象如圖所示，若兩個正數a、b滿足f（2a+b）＜2，則 
的取值范圍是（ ）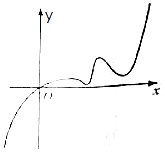 
A.（ 
，2）
B.（﹣∞， ）∪（2，+∞）
C.（2，+∞）
D.（﹣∞， ）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
