
已知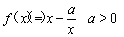 ,
,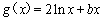 ,且直線
,且直線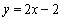 與曲線
與曲線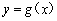 相切.
相切.
(1)若對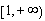 內的一切實數(shù)
內的一切實數(shù)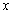 ,不等式
,不等式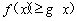 恒成立,求實數(shù)
恒成立,求實數(shù)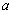 的取值范圍;
的取值范圍;
(2)當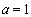 時,求最大的正整數(shù)
時,求最大的正整數(shù)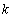 ,使得對
,使得對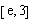 (
(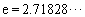 是自然對數(shù)的底數(shù))內的任意
是自然對數(shù)的底數(shù))內的任意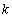 個實數(shù)
個實數(shù)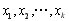 都有
都有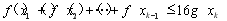 成立;
成立;
(3)求證: .
.
(1)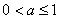 (2)見解析(3)見解析
(2)見解析(3)見解析
【解析】(1)設點 為直線
為直線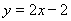 與曲線
與曲線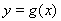 的切點,則有
的切點,則有 .(*)
.(*)
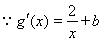 ,
,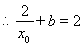 . (**)
. (**)
由(*)、(**)兩式,解得 ,
, .……………………………2分
.……………………………2分
由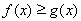 整理,得
整理,得 ,
,
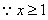 ,
, 要使不等式
要使不等式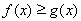 恒成立,必須
恒成立,必須 恒成立.
恒成立.
設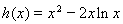 ,
,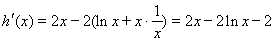 ,
,
 ,
, 當
當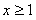 時,
時,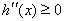 ,則
,則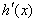 是增函數(shù),
是增函數(shù),
 ,
,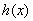 是增函數(shù),
是增函數(shù), ,
, .…………………5分
.…………………5分
因此,實數(shù)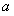 的取值范圍是
的取值范圍是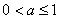 .………………………………………6分
.………………………………………6分
(2)當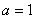 時,
時,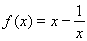 ,
,
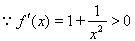 ,
, 在
在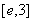 上是增函數(shù),
上是增函數(shù),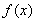 在
在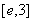 上的最大值為
上的最大值為 .
.
要對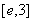 內的任意
內的任意 個實數(shù)
個實數(shù) 都有
都有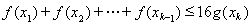
成立,必須使得不等式左邊的最大值小于或等于右邊的最小值,
 當
當 時不等式左邊取得最大值,
時不等式左邊取得最大值, 時不等式右邊取得最小值.
時不等式右邊取得最小值.
 ,解得
,解得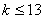 .
.
因此,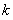 的最大值為
的最大值為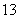 .………………………………………10分
.………………………………………10分
(3)證明(法一):當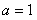 時,根據(jù)(1)的推導有,
時,根據(jù)(1)的推導有, 時,
時,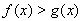 ,
,
即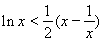 .………………………………………………………11分
.………………………………………………………11分
令 ,得
,得 ,
,
化簡得 ,………………………………13分
,………………………………13分
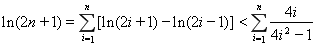 .………………………14分
.………………………14分
(法二)數(shù)學歸納法:當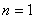 時,左邊=
時,左邊= ,右邊=
,右邊=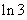 ,
,
根據(jù)(1)的推導有, 時,
時, ,即
,即 .
.
令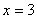 ,得
,得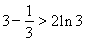 ,即
,即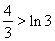 .
.
因此,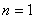 時不等式成立.………………………………11分
時不等式成立.………………………………11分
(另【解析】 ,
,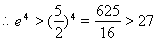 ,
, ,即
,即 .)
.)
假設當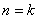 時不等式成立,即
時不等式成立,即 ,
,
則當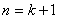 時,
時, ,
,
要證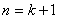 時命題成立,即證
時命題成立,即證 ,
,
即證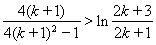 .
.
在不等式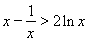 中,令
中,令 ,得
,得
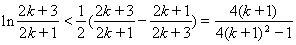 .
.
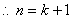 時命題也成立.………………………………………13分
時命題也成立.………………………………………13分
根據(jù)數(shù)學歸納法,可得不等式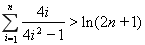 對一切
對一切 成立. …14分
成立. …14分
本題主要考查函數(shù)的性質、導數(shù)運算法則、導數(shù)的幾何意義及其應用、不等式的求解與證明、數(shù)學歸納法等綜合知識,考查學生的計算推理能力及分析問題、解決問題的能力及創(chuàng)新意識.


 芝麻開花課程新體驗系列答案
芝麻開花課程新體驗系列答案科目:高中數(shù)學 來源:2014年高考數(shù)學全程總復習課時提升作業(yè)七十二第十章第九節(jié)練習卷(解析版) 題型:填空題
某畢業(yè)生參加人才招聘會,分別向甲、乙、丙三個公司投遞了個人簡歷.假定該畢業(yè)生得到甲公司面試的概率為 ,得到乙、丙兩公司面試的概率均為p,且三個公司是否讓其面試是相互獨立的.記X為該畢業(yè)生得到面試的公司個數(shù).若P(X=0)=
,得到乙、丙兩公司面試的概率均為p,且三個公司是否讓其面試是相互獨立的.記X為該畢業(yè)生得到面試的公司個數(shù).若P(X=0)=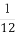 ,則隨機變量X的數(shù)學期望E(X)= .
,則隨機變量X的數(shù)學期望E(X)= .
查看答案和解析>>
科目:高中數(shù)學 來源:2014年高考數(shù)學全程總復習課時提升作業(yè)七十一第十章第八節(jié)練習卷(解析版) 題型:解答題
某市職教中心組織廚師技能大賽,大賽依次設基本功(初賽)、面點制作(復賽)、熱菜烹制(決賽)三個輪次的比賽,已知某選手通過初賽、復賽、決賽的概率分別是 ,
, ,
, 且各輪次通過與否相互獨立.
且各輪次通過與否相互獨立.
(1)設該選手參賽的輪次為ξ,求ξ的分布列.
(2)對于(1)中的ξ,設“函數(shù)f(x)=3sin π(x∈R)是偶函數(shù)”為事件D,求事件D發(fā)生的概率.
π(x∈R)是偶函數(shù)”為事件D,求事件D發(fā)生的概率.
查看答案和解析>>
科目:高中數(shù)學 來源:2014年高中數(shù)學全國各省市理科導數(shù)精選22道大題練習卷(解析版) 題型:解答題
已知向量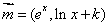 ,
,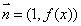 ,
,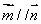 (
(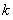 為常數(shù),
為常數(shù), 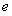 是自然對數(shù)的底數(shù)),曲線
是自然對數(shù)的底數(shù)),曲線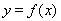 在點
在點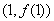 處的切線與
處的切線與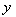 軸垂直,
軸垂直,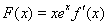 .
.
(Ⅰ)求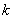 的值及
的值及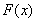 的單調區(qū)間;
的單調區(qū)間;
(Ⅱ)已知函數(shù) (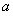 為正實數(shù)),若對于任意
為正實數(shù)),若對于任意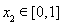 ,總存在
,總存在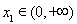 , 使得
, 使得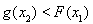 ,求實數(shù)
,求實數(shù)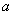 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源:2014年高中數(shù)學全國各省市理科導數(shù)精選22道大題練習卷(解析版) 題型:解答題
若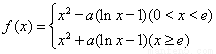 ,其中
,其中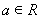 .
.
(1)當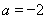 時,求函數(shù)
時,求函數(shù)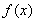 在區(qū)間
在區(qū)間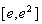 上的最大值;
上的最大值;
(2)當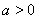 時,若
時,若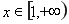 ,
,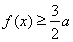 恒成立,求
恒成立,求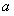 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源:2014年陜西省咸陽市高考模擬考試(一)理科數(shù)學試卷(解析版) 題型:解答題
如圖,四邊形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2.又AC=1,∠ACB=120°,AB⊥PC,直線AM與直線PC所成的角為60°.
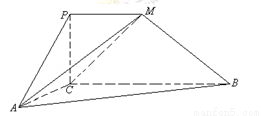
(1)求證:PC⊥AC;
(2)求二面角M﹣AC﹣B的余弦值;
(3)求點B到平面MAC的距離.
查看答案和解析>>
科目:高中數(shù)學 來源:2014年陜西省咸陽市高考模擬考試(一)理科數(shù)學試卷(解析版) 題型:填空題
設命題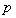 :實數(shù)
:實數(shù)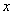 滿足
滿足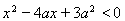 ,其中
,其中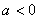 ;命題
;命題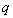 :實數(shù)
:實數(shù)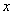 滿足
滿足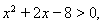 且
且 的必要不充分條件,則實數(shù)
的必要不充分條件,則實數(shù)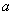 的取值范圍是 .
的取值范圍是 .
查看答案和解析>>
科目:高中數(shù)學 來源:2014年廣東省廣州市畢業(yè)班綜合測試一理科數(shù)學試卷(解析版) 題型:解答題
已知函數(shù) 的圖象經(jīng)過點
的圖象經(jīng)過點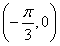 .
.
(1)求實數(shù)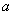 的值;
的值;
(2)設 ,求函數(shù)
,求函數(shù)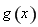 的最小正周期與單調遞增區(qū)間.
的最小正周期與單調遞增區(qū)間.
查看答案和解析>>
科目:高中數(shù)學 來源:2013-2014學年(安徽專用)高考數(shù)學(文)仿真模擬卷2練習卷(解析版) 題型:解答題
某高校組織自主招生考試,其有2 000名學生報名參加了筆試,成績均介于195分到275分之間,從中隨機抽取50名同學的成績進行統(tǒng)計,將統(tǒng)計結果按如下方式分成八組:第一組[195,205),第二組[205,215),……,第八組[265,275).如圖是按上述分組方法得到的頻率分布直方圖.
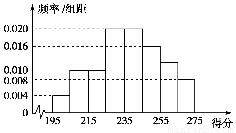
(1)從這2 000名學生中,任取1人,求這個人的分數(shù)在255~265之間的概率約是多少?
(2)求這2 000名學生的平均分數(shù);
(3)若計劃按成績取1 000名學生進入面試環(huán)節(jié),試估計應將分數(shù)線定為多少?
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com