
【題目】已知三棱錐![]() ,底面
,底面![]() 為邊長為2的正三角形,側(cè)棱
為邊長為2的正三角形,側(cè)棱![]() ,
,![]()
(1)求證:![]() ;
;
(2)求![]() 點到平面
點到平面![]() 的距離.
的距離.

【答案】(1)見解析;(2)![]() .
.
【解析】分析:(1)取AC的中點為O,由題意可證得SO⊥AC,OB⊥AC,由線面垂直的判斷定理可得AC⊥平面SOB,則AC⊥SB;
(2)由(1)可知△ASC為直角三角形,由幾何關(guān)系可證得SO⊥平面ABC,轉(zhuǎn)化頂點利用體積相等可求得求![]() 點到平面
點到平面![]() 的距離為
的距離為![]() .
.
詳解:(1)取AC的中點為O,∵SA=SC∴SO⊥AC AB=BC,∴OB⊥AC,
又∵SO與OB相交于O,OS平面SOB OB平面SOB,
∴AC⊥平面SOB 又∵SB平面SOB,
∴AC⊥SB;
(2)由(1)可知,SA=SC=![]() ,AC=2,∴△ASC為Rt△,
,AC=2,∴△ASC為Rt△,
∴SO=1 在正三角形ABC中,OB=![]() , SB=2 , SO2+OB2=SB2,
, SB=2 , SO2+OB2=SB2,
∴SO⊥OB∴SO⊥平面ABC,
VS﹣ABC=![]() ,
,
S△SBC=![]() ,
,
∵VS﹣ABC=VA﹣SBC ![]()
![]() ,h=
,h=![]() .
.


 作業(yè)輔導(dǎo)系列答案
作業(yè)輔導(dǎo)系列答案 同步學(xué)典一課多練系列答案
同步學(xué)典一課多練系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 的定義域為
的定義域為![]() ,且對任意的
,且對任意的![]() 有
有![]() . 當(dāng)
. 當(dāng)![]() 時,
時,![]() ,
,![]() .
.
(1)求![]() 并證明
并證明![]() 的奇偶性;
的奇偶性;
(2)判斷![]() 的單調(diào)性并證明;
的單調(diào)性并證明;
(3)求![]() ;若
;若![]() 對任意
對任意![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD中,底面ABCD為菱形,且PA=PD=DA=2,∠BAD=60°
(I)求證:PB⊥AD;
(II)若PB=![]() , 求二面角A﹣PD﹣C的余弦值.
, 求二面角A﹣PD﹣C的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
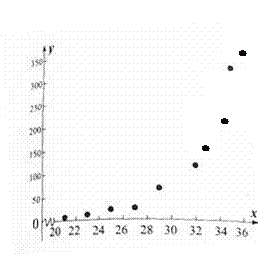
【題目】經(jīng)觀測,某昆蟲的產(chǎn)卵數(shù)y與溫度x有關(guān),現(xiàn)將收集到的溫度xi和產(chǎn)卵數(shù)yi(i=1,2,…,10)的10組觀測數(shù)據(jù)作了初步處理,得到如下圖的散點圖及一些統(tǒng)計量表.
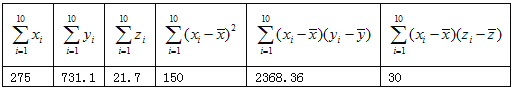
表中![]() ,
, ![]()
(1)根據(jù)散點圖判斷, ![]() ,
, ![]() 與
與![]() 哪一個適宜作為y與x之間的回歸方程模型?(給出判斷即可,不必說明理由)
哪一個適宜作為y與x之間的回歸方程模型?(給出判斷即可,不必說明理由)
(2)根據(jù)(1)的判斷結(jié)果及表中數(shù)據(jù).
①試求y關(guān)于x回歸方程;
②已知用人工培養(yǎng)該昆蟲的成本h(x)與溫度x和產(chǎn)卵數(shù)y的關(guān)系為h(x)=x(lny﹣2.4)+170,當(dāng)溫度x(x取整數(shù))為何值時,培養(yǎng)成本的預(yù)報值最小?
附:對于一組數(shù)據(jù)(u1,v1),(u2,v2),…(un,vn),其回歸直線v=α+βu的斜率和截距的最小二乘估計分別為β=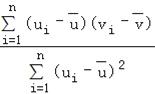 ,α=
,α=![]() ﹣β
﹣β![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知△ABC的內(nèi)角A,B,C滿足sin2A+sin(A﹣B+C)=sin(C﹣A﹣B)+ ![]() ,面積S滿足1≤S≤2,記a,b,c分別為A,B,C所對的邊,在下列不等式一定成立的是( )
,面積S滿足1≤S≤2,記a,b,c分別為A,B,C所對的邊,在下列不等式一定成立的是( )
A.bc(b+c)>8
B.ab(a+b)>16 ![]()
C.6≤abc≤12
D.12≤abc≤24
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】以直角坐標(biāo)系的原點![]() 為極點,
為極點, ![]() 軸正半軸為極軸,并在兩種坐標(biāo)系中取相同的長度單位,已知直線
軸正半軸為極軸,并在兩種坐標(biāo)系中取相同的長度單位,已知直線![]() 的參數(shù)方程為
的參數(shù)方程為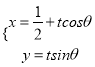 ,(
,( ![]() 為參數(shù),
為參數(shù), ![]() ),曲線
),曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)設(shè)直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
, ![]() 兩點,當(dāng)
兩點,當(dāng)![]() 變化時,求
變化時,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某幾何體的三視圖(單位:cm)如圖所示,則此幾何體的表面積是( ) 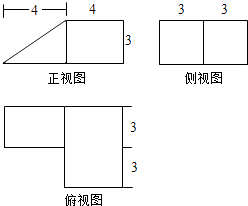
A.90cm2
B.129cm2
C.132cm2
D.138cm2
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】假設(shè)每一架飛機的引擎在飛行中出現(xiàn)故障率為![]() ,且各引擎是否有故障是獨立的,已知4引擎飛機中至少有3個引擎正常運行,飛機就可成功飛行;2引擎飛機要2個引擎全部正常運行,飛機也可成功飛行,要使4引擎飛機比2引擎飛機更安全,則
,且各引擎是否有故障是獨立的,已知4引擎飛機中至少有3個引擎正常運行,飛機就可成功飛行;2引擎飛機要2個引擎全部正常運行,飛機也可成功飛行,要使4引擎飛機比2引擎飛機更安全,則![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】定義在![]() 上的函數(shù)
上的函數(shù)![]() ,如果滿足:對任意
,如果滿足:對任意![]() ,存在常數(shù)
,存在常數(shù)![]() ,都有
,都有![]() 成立,則稱
成立,則稱![]() 是
是![]() 上的有界函數(shù),其中
上的有界函數(shù),其中![]() 稱為函數(shù)
稱為函數(shù)![]() 的一個上界.已知函數(shù)
的一個上界.已知函數(shù)![]() ,
, ![]() .
.
(1)若函數(shù)![]() 為奇函數(shù),求實數(shù)
為奇函數(shù),求實數(shù)![]() 的值;
的值;
(2)在(1)的條件下,求函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的所有上界構(gòu)成的集合;
上的所有上界構(gòu)成的集合;
(3)若函數(shù)![]() 在
在![]() 上是以3為上界的有界函數(shù),求實數(shù)
上是以3為上界的有界函數(shù),求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com