從0,1,2， ，10中挑選若干個不同的數(shù)字填滿圖中每一個圓圈稱為一種“填法”，若各條線段相連的兩個圓圈內(nèi)的數(shù)字之差的絕對值各不相同，則稱這樣的填法為“完美填法”。
試問：對圖1和圖2是否存在完美填法？若存在，請給出一種完美填法；若不存在，請說明理由。
對圖1，上述填法即為完美（答案不唯一）。
對于圖2不存在完美填法。
解析試題分析：對圖1，上述填法即為完美（答案不唯一）。 10分
對于圖2不存在完美填法。因為圖中一共有10條連線，因此各連線上兩數(shù)之差的絕對值恰好為，1,2,3， ，10， 15分
其和
為奇數(shù)。 20分
另一方面，圖中每一個圓圈所連接的連線數(shù)都為偶數(shù)條。即每一個圓圈內(nèi)德數(shù)在上述S的表達式中出現(xiàn)偶數(shù)次。因此S應為偶數(shù)，矛盾。 25分
所以，不存在完美填法。
考點：新定義問題，實數(shù)絕對值的性質(zhì)。
點評：難題，理解新定義內(nèi)容是正確解題的關(guān)鍵。對圖表的識別能力及轉(zhuǎn)化與化歸思想要求較高。
科目：高中數(shù)學 來源： 題型：解答題
設
是由
個實數(shù)組成的
行
列的數(shù)表，如果某一行（或某一列）各數(shù)之和為負數(shù)，則改變該行（或該列）中所有數(shù)的符號，稱為一次“操作”.
(Ⅰ) 數(shù)表如表1所示，若經(jīng)過兩次“操作”，使得到的數(shù)表每行的各數(shù)之和與每列的各數(shù)之和均為非負實數(shù)，請寫出每次“操作”后所得的數(shù)表（寫出一種方法即可）；
表1
| 1 | 2 | 3 |  |
 | 1 | 0 | 1 |
如表2所示，若經(jīng)過任意一次“操作”以后，便可使得到的數(shù)表每行的各數(shù)之和與每列的各數(shù)之和均為非負整數(shù)，求整數(shù)
的所有可能值；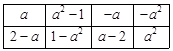
個整數(shù)組成的行列的任意一個數(shù)表，能否經(jīng)過有限次“操作”以后，使得到的數(shù)表每行的各數(shù)之和與每列的各數(shù)之和均為非負整數(shù)？請說明理由. 查看答案和解析>>
科目：高中數(shù)學 來源： 題型：解答題
設函數(shù)
對任意實數(shù)x 、y都有
，
（1）求
的值；
（2）若
，求
、
、
的值；
（3）在（2）的條件下，猜想
的表達式，并用數(shù)學歸納法加以證明。
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：單選題
若（a－4i）i=b－i，（a，b∈R，i為虛數(shù)單位），則復數(shù)z=a+bi在復平面內(nèi)的對應點位于（ ）
| A．第一象限 | B．第二象限 | C．第三象限 | D．第四象限 |
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
使得
對一切
恒成立？若存在，求出
－
≥a＋
－2.
.
等于( )
i