Question

【題目】（文）已知點D（1， ）在雙曲線C： =1（a＞0，b＞0）上，且雙曲線的一條漸近線的方程是 x+y=0．
（1）求雙曲線C的方程；
（2）若過點（0，1）且斜率為k的直線l與雙曲線C有兩個不同交點，求實數k的取值范圍；
（3）設（2）中直線l與雙曲線C交于A、B兩個不同點，若以線段AB為直徑的圓經過坐標原點，求實數k的值．

Answer 1

【答案】
（1）解：由題知，有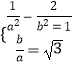

解得

因此，所求雙曲線C的方程是

（2）解：∵直線l過點（0，1）且斜率為k，

∴直線l：y=kx+1．

代入雙曲線方程得（3﹣k2）x2﹣2kx﹣2=0．

又直線l與雙曲線C有兩個不同交點，

∴3﹣k2≠0且△=（﹣2k）2+8（3﹣k2）＞0

解得k∈（﹣ ，﹣ ）∪（﹣ ， ）∪（ ， ）

（3）解：設點A、B的坐標為（x1，y1）、（x2，y2）．

由（2）可得x1+x2= ，x1x2=

又以線段AB為直徑的圓經過坐標原點，

則kOAkOB=﹣1，即x1x2+y1y2=0，

∴x1x2+（kx1+1）（kx2+1）=0，

即（k2+1）x1x2+k（x1+x2）+1=0，

∴ ，解得k=±1．

又k=±1滿足3﹣k2≠0且△=（﹣2k）2+8（3﹣k2）＞0，

∴所求實數k=±1

【解析】（1）點D（1， ）代入雙曲線方程，結合且雙曲線的一條漸近線的方程是 x+y=0，建立方程，求出a，b，即可求雙曲線C的方程；（2）直接聯立直線與雙曲線方程，化為關于x的一元二次方程，利用根的判別式，即可求實數k的取值范圍；（3）存在實數k，使得以線段AB為直徑的圓經過坐標原點轉化為kOAkOB=﹣1，即x1x2+y1y2=0，整理后代入根與系數關系求解實數k的值．