【題目】在正四面體
中，
分別是
的中點，下面四個結(jié)論：
①
//平面
②
平面
③平面
平面
④平面
平面
其中正確結(jié)論的序號是______________.
【答案】①②④
【解析】
如圖所示,由已知條件利用線面平行,線面垂直,面面垂直的判定直接推導(dǎo)即可得出答案.
如圖所示,在正四面體P-ABC中,D,F分別是AB,CA的中點,則DF//BC,
因為
平面PDF,BC平面PDF,所以BC//平面PDF,故①正確;
由PB=PC,AB=AC,E為中點,得
,所以
平面PAE,由DF//BC得DF
平面PAE,故②正確;
過P作PO平面ABC,垂足為O,由題意得O點為底面△ABC的中心,且點O在AE上,AO=
AE,
設(shè)AE與DF的交點為M,則由AM=
AE,故點O,M不重合,則平面PDF和平面ABC不垂直,故③不正確;
由②得平面PAE,BC平面PBC,所以平面PBC平面PAE,故④正確,綜上可得正確的序號為①②④.
故答案為:①②④.
口算能手系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓
的焦距為
，且
，圓
與
軸交于點
，
，
為橢圓
上的動點，
，
面積最大值為
.
（1）求圓
與橢圓的方程；
（2）圓的切線
交橢圓于點
，
，求
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某賽季甲、乙兩名籃球運動員各13場比賽得分情況用莖葉圖表示如圖：
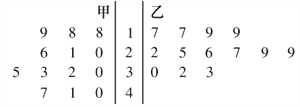
根據(jù)上圖，對這兩名運動員地成績進行比較，下列四個結(jié)論中，不正確的是
A. 甲運動員得分的極差大于乙運動員得分的極差
B. 甲運動員得分的中位數(shù)大于乙運動員得分的中位數(shù)
C. 甲運動員的得分平均值大于乙運動員的得分平均值
D. 甲運動員的成績比乙運動員的成績穩(wěn)定
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知
是橢圓
的左、右焦點，點
在橢圓
上，線段
與
軸的交點
滿足
.
（1）求橢圓的標(biāo)準(zhǔn)方程；
（2）過點
作不與
軸重合的直線
，設(shè)與圓
相交于
兩點，與橢圓相交于
兩點，當(dāng)
且
時，求
的面積
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
，
為函數(shù)
的導(dǎo)函數(shù)．
（1）設(shè)函數(shù)的圖象與
軸交點為
，曲線
在點處的切線方程是
，求
，
的值；
（2）若函數(shù)
，求函數(shù)
的單調(diào)區(qū)間．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】下列命題中正確的是( )
A.若a，b是兩條直線，且a∥b，那么a平行于經(jīng)過b的任何平面
B.若直線a和平面α滿足a∥α，那么a與α內(nèi)的任何直線平行
C.平行于同一條直線的兩個平面平行
D.若直線a，b和平面α滿足a∥b，a∥α，b不在平面α內(nèi)，則b∥α
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，已知點P是平行四邊形ABCD所在平面外一點，M、N分別是AB、PC的中點．
（1）求證：MN∥平面PAD；
（2）在PB上確定一個點Q，使平面MNQ∥平面PAD.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某單位從一所學(xué)校招收某類特殊人才,對
位已經(jīng)選拔入圍的學(xué)生進行運動協(xié)調(diào)能力和邏輯思維能力的測試,其測試結(jié)果如下表:
例如,表中運動協(xié)調(diào)能力良好且邏輯思維能力一般的學(xué)生有
人.由于部分?jǐn)?shù)據(jù)丟失,只知道從這位參加測試的學(xué)生中隨機抽取一位,抽到運動協(xié)調(diào)能力或邏輯思維能力優(yōu)秀的學(xué)生的概率為
.
（Ⅰ）求
的值;
（Ⅱ）從參加測試的位學(xué)生中任意抽取
位,求其中至少有一位運動協(xié)調(diào)能力或邏輯思維能力優(yōu)秀的學(xué)生的概率;
（III）從參加測試的位學(xué)生中任意抽取位,設(shè)運動協(xié)調(diào)能力或邏輯思維能力優(yōu)秀的學(xué)生人數(shù)為
,求隨機變量的分布列.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
，在點
處的切線方程為
，求（1）實數(shù)
的值；（2）函數(shù)
的單調(diào)區(qū)間以及在區(qū)間
上的最值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com