
【題目】求下列橢圓的標準方程:
(1)焦點在![]() 軸上,離心率
軸上,離心率![]() ,且經過點
,且經過點 ;
;
(2)以坐標軸為對稱軸,且長軸長是短軸長的![]() 倍,并且過點
倍,并且過點![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)由焦點在![]() 軸上,可設橢圓的標準方程為
軸上,可設橢圓的標準方程為![]() ,將點A代入方程,由離心率與橢圓的系數關系整理得方程,由上述兩個方程解得
,將點A代入方程,由離心率與橢圓的系數關系整理得方程,由上述兩個方程解得![]() ,代入所設方程得答案;
,代入所設方程得答案;
(2)分類討論焦點在![]() 軸與
軸與![]() 軸,利用待定系數法設出方程,代入點坐標可得方程,由已知長軸長是短軸長的
軸,利用待定系數法設出方程,代入點坐標可得方程,由已知長軸長是短軸長的![]() 倍又可構建方程,聯立方程組求得所設方程系數,既得答案.
倍又可構建方程,聯立方程組求得所設方程系數,既得答案.
(1)因為焦點在![]() 軸上,即設橢圓的標準方程為
軸上,即設橢圓的標準方程為![]() ,
,
∵橢圓經過點 ,
,![]() .①,
.①,
由已知![]() ,即
,即![]() .②,
.②,
把②代入①,得![]() ,解得
,解得![]() ,
,
∴橢圓的標準方程為![]() .
.
(2)若焦點在![]() 軸上,設方程為
軸上,設方程為![]()
因為橢圓過點![]() ,所以
,所以![]() ,又
,又![]() ,
,![]()
橢圓的標準方程為![]() ,
,
若焦點在![]() 軸上,設方程為
軸上,設方程為![]() 因為橢圓過點
因為橢圓過點![]() ,,所以
,,所以![]() ,又
,又![]() ,
,![]() ∴橢圓的方程為
∴橢圓的方程為![]()
綜上,所求的橢圓方程是 ![]() 或
或![]()


科目:高中數學 來源: 題型:
【題目】已知某企業生產某種產品的年固定成本為200萬元,且每生產1噸該產品需另投入12萬元,現假設該企業在一年內共生產該產品![]() 噸并全部銷售完.每噸的銷售收入為
噸并全部銷售完.每噸的銷售收入為![]() 萬元,且
萬元,且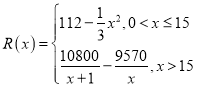 .
.
(1)求該企業年總利潤![]() (萬元)關于年產量
(萬元)關于年產量![]() (噸)的函數關系式;
(噸)的函數關系式;
(2)當年產量為多少噸時,該企業在這一產品的生產中所獲年總利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右頂點為
的右頂點為![]() ,
,![]() 為上頂點,點
為上頂點,點![]() 為橢圓
為橢圓![]() 上一動點.
上一動點.
(1)若![]() ,求直線
,求直線![]() 與
與![]() 軸的交點坐標;
軸的交點坐標;
(2)設![]() 為橢圓
為橢圓![]() 的右焦點,過點
的右焦點,過點![]() 與
與![]() 軸垂直的直線為
軸垂直的直線為![]() ,
,![]() 的中點為
的中點為![]() ,過點
,過點![]() 作直線
作直線![]() 的垂線,垂足為
的垂線,垂足為![]() ,求證:直線
,求證:直線![]() 與直線
與直線![]() 的交點在橢圓
的交點在橢圓![]() 上.
上.
查看答案和解析>>
科目:高中數學 來源: 題型:
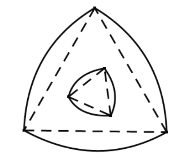
【題目】勒洛三角形是具有類似圓的“定寬性”的曲線,它是由德國機械工程專家、機構運動學家勒洛首先發現,其作法是:以等邊三角形每個頂點為圓心,以邊長為半徑,在另兩個頂點間作一段弧,三段弧圍成的曲邊三角形就是勒洛三角形.如圖中的兩個勒洛三角形,它們所對應的等邊三角形的邊長比為![]() ,若從大的勒洛三角形中隨機取一點,則此點取自小勒洛三角形內的概率為( )
,若從大的勒洛三角形中隨機取一點,則此點取自小勒洛三角形內的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】空氣質量指數AQI是反映空氣質量狀況的指數,AQI指數值越小,表明空氣質量越好,其對應關系如表:
AQI指數值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 |
|
空氣質量 | 優 | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴重污染 |
如圖是某市12月1日-20日AQI指數變化趨勢:

下列敘述正確的是( )
A.這20天中AQI指數值的中位數略高于100
B.這20天中的中度污染及以上的天數占![]()
C.該市12月的前半個月的空氣質量越來越好
D.總體來說,該市12月上旬的空氣質量比中旬的空氣質量好
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,點P到兩點(0,![]() ),(0,
),(0,![]() )的距離之和為4,設點P的軌跡為C,直線y=kx+1與A交于A,B兩點.
)的距離之和為4,設點P的軌跡為C,直線y=kx+1與A交于A,B兩點.
(1)寫出C的方程;
(2)若![]() ,求k的值.
,求k的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年春節前后,一場突如其來的新冠肺炎疫情在全國蔓延.疫情就是命令,防控就是責任.在黨中央的堅強領導和統一指揮下,全國人民眾志成城、團結一心,掀起了一場堅決打贏疫情防控阻擊戰的人民戰爭.下圖表展示了2月14日至29日全國新冠肺炎疫情變化情況,根據該折線圖,下列結論正確的是( )
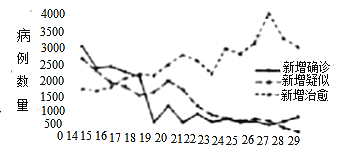
A.16天中每日新增確診病例數量呈下降趨勢且19日的降幅最大
B.16天中每日新增確診病例的中位數小于新增疑似病例的中位數
C.16天中新增確診、新增疑似、新增治愈病例的極差均大于2000
D.19日至29日每日新增治愈病例數量均大于新增確診與新增疑似病例之和
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com