
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,離心率為
,離心率為![]() ,過點
,過點![]() 的直線與橢圓
的直線與橢圓![]() 相交于
相交于![]() 兩點,且
兩點,且![]() 的周長為8.
的周長為8.
(1)求橢圓![]() 的方程;
的方程;
(2)若經過原點![]() 的直線與橢圓
的直線與橢圓![]() 相交于
相交于![]() 兩點,且
兩點,且![]() ,試判斷
,試判斷![]() 是否為定值?若為定值,試求出該定值;否則,請說明理由.
是否為定值?若為定值,試求出該定值;否則,請說明理由.
【答案】(1) 橢圓![]() 的方程為
的方程為![]() (2)見解析.
(2)見解析.
【解析】試題分析:(1)由題意知, ![]() 的周長,求得
的周長,求得![]() 的值,進而得到
的值,進而得到![]() 的值,從而求得橢圓的方程;
的值,從而求得橢圓的方程;
(2)①當直線![]() 在斜率不存在時,把
在斜率不存在時,把![]() 代入橢圓方程,即可求解
代入橢圓方程,即可求解![]() 的值;
的值;
②當直線![]() 的斜率
的斜率![]() 存在時,設其方程為
存在時,設其方程為![]() ,聯立方程組,求得
,聯立方程組,求得![]() ,利用弦長公式,求解
,利用弦長公式,求解![]() ,再根據因為
,再根據因為![]() ,所以直線
,所以直線![]() 的方程為
的方程為![]() ,聯立方程組,進而求得則
,聯立方程組,進而求得則![]() ,即可得到結論.
,即可得到結論.
試題解析:
(1)由題意知, ![]() 的周長為
的周長為![]() ,所以
,所以![]() ,
,
又橢圓![]() 的離心率為
的離心率為![]() ,所以
,所以![]() ,
,
所以![]() ,故橢圓
,故橢圓![]() 的方程為
的方程為![]() ;
;
(2)①當直線![]() 在斜率不存在時,其方程為
在斜率不存在時,其方程為![]() ,代入橢圓方程得
,代入橢圓方程得![]() ,
,
不妨設![]() ,則
,則![]() ,
,
因為![]() ,所以直線
,所以直線![]() 的方程為
的方程為![]() ,代入橢圓方程得
,代入橢圓方程得![]() ,
,
不妨設![]() ,則
,則![]() ,
,
所以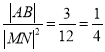 ;
;
②當直線![]() 的斜率
的斜率![]() 存在時,設其方程為
存在時,設其方程為![]() ,
,
由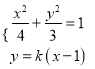 消去
消去![]() 得
得![]() ,
,
則![]() ,
,
![]() ,則
,則![]() ,
,
因為![]() ,所以直線
,所以直線![]() 的方程為
的方程為![]() ,設
,設![]() ,
,
由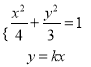 消去
消去![]() 得
得![]() ,則
,則![]() ,
,
則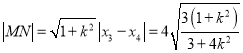 ,
,
所以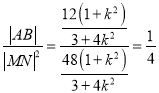 ,綜上所述,
,綜上所述, ![]() 為定值
為定值![]()


科目:高中數學 來源: 題型:
【題目】如圖,已知平面![]()
![]() 平面
平面![]() ,
, ![]() 與
與![]() 分別是棱長為1與2的正三角形,
分別是棱長為1與2的正三角形, ![]() //
// ![]() ,四邊形
,四邊形![]() 為直角梯形,
為直角梯形, ![]() //
// ![]() ,
, ![]() ,點
,點![]() 為
為![]() 的重心,
的重心, ![]() 為
為![]() 中點,
中點, ![]() .
.

(Ⅰ)當![]() 時,求證:
時,求證: ![]() //平面
//平面![]() ;
;
(Ⅱ)若直線![]() 與
與![]() 所成角為
所成角為![]() ,試求二面角
,試求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,有一塊矩形空地,要在這塊空地上開辟一個內接四邊形為綠地,使其四個頂點分別落在矩形的四條邊上,已知![]() 且
且![]() 設
設![]() ,綠地面積為
,綠地面積為![]() .
.
(1)寫出![]() 關于
關于![]() 的函數關系式,并指出這個函數的定義域.
的函數關系式,并指出這個函數的定義域.
(2)當![]() 為何值時,綠地面積
為何值時,綠地面積![]() 最大?
最大?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,a,b,c分別為A,B,C所對邊,a+b=4,(2﹣cosA)tan ![]() =sinA.
=sinA.
(1)求邊長c的值;
(2)若E為AB的中點,求線段EC的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】聯合國教科文組織規定,每年的4月23日是“世界讀書日”.某校研究生學習小組為了解本校學生的閱讀情況,隨機調查了本校400名學生在這一天的閱讀時間![]() (單位:分鐘),將時間數據分成5組:
(單位:分鐘),將時間數據分成5組:![]() ,并整理得到如下頻率分布直方圖.
,并整理得到如下頻率分布直方圖.
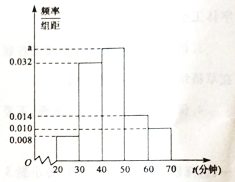
(1)求![]() 的值;
的值;
(2)試估計該學校所有學生在這一天的平均閱讀時間;
(3)若用分層抽樣的方法從這400名學生中抽取50人參加交流會,則在閱讀時間為![]() 的兩組中分別抽取多少人?
的兩組中分別抽取多少人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左右焦點分別為
的左右焦點分別為![]() ,上頂點為
,上頂點為![]() ,若直線
,若直線![]() 的斜率為1,且與橢圓的另一個交點為
的斜率為1,且與橢圓的另一個交點為![]() ,
, ![]() 的周長為
的周長為![]() .
.
(1)求橢圓的標準方程;
(2)過點![]() 的直線
的直線![]() (直線
(直線![]() 的斜率不為1)與橢圓交于
的斜率不為1)與橢圓交于![]() 兩點,點
兩點,點![]() 在點
在點![]() 的上方,若
的上方,若![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角梯形ABCD中,AD∥BC,∠A=90°,AB=2AD,若將△ABD沿直線BD折成△A′BD,使得A′D⊥BC,則直線A′B與平面BCD所成角的正弦值是 . 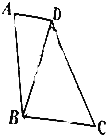
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線的頂點是坐標原點![]() ,焦點
,焦點![]() 在
在![]() 軸的正半軸上,過焦點
軸的正半軸上,過焦點![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 與拋物線交于
與拋物線交于![]() 兩點,且滿足
兩點,且滿足![]() .
.
(1)求拋物線的方程;
(2)已知![]() 為拋物線上一點,若點
為拋物線上一點,若點![]() 位于
位于![]() 軸下方且
軸下方且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《城市規劃管理意見》中提出“新建住宅原則上不再建設封閉住宅小區,已建成的住宅小區和單位大院逐步打開”,此消息在網上一石激起千層浪.各種說法不一而足,為了了解居民對“開放小區”認同與否,從[25,55]歲人群中隨機抽取了n人進行問卷調查,得如下數據:
組數 | 分組 | 認同人數 | 認同人數占 |
第一組 | [25,30) | 120 | 0.6 |
第二組 | [30,35) | 195 | p |
第三組 | [35,40) | 100 | 0.5 |
第四組 | [40,45) | a | 0.4 |
第五組 | [45,50) | 30 | 0.3 |
第六組 | [50,55) | 15 | 0.3 |
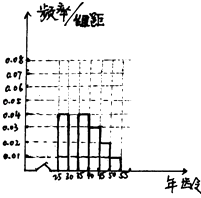
(1)完成所給頻率分布直方圖,并求n,a,p.
(2)若從[40,45),[45,50)兩個年齡段中的“認同”人群中,按分層抽樣的方法抽9人參與座談會,然后從這9人中選2名作為組長,組長年齡在[40,45)內的人數記為ξ,求隨機變量ξ的分布列和期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com