
【題目】(1)設a>b>0,試比較![]() 與
與![]() 的大小.
的大小.
(2)若關于x的不等式(2x-1)2<ax2的解集中整數恰好有3個,求實數a的取值范圍
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)利用作差法或作商法證明即可.
(2)將不等式![]() 整理成二次不等式的形式,再根據解集中整數恰好有3個,分析二次方程的零點的范圍即可知解集中整數解一定是1,2,3,再列出二次方程零點滿足的范圍即可.
整理成二次不等式的形式,再根據解集中整數恰好有3個,分析二次方程的零點的范圍即可知解集中整數解一定是1,2,3,再列出二次方程零點滿足的范圍即可.
解:(1)(作差法)
![]() -
-![]() =
=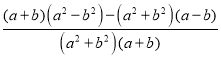
=
=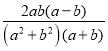 .
.
∵a>b>0,∴a+b>0,a-b>0,2ab>0,a2+b2>0,
∴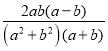 >0,∴
>0,∴![]()
![]()
(作商法)
∵a>b>0,∴![]() >0,
>0,![]() >0,2ab>0,
>0,2ab>0,
∴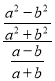 =
=![]() =
=![]() =1+
=1+![]() >1
>1
![]()
(2)不等式(2x-1)2<ax2等價于(4-a)x2-4x+1<0,∵不等式(2x-1)2<ax2的解集中整數恰好有3個,∴![]()
解得0<a<4,
∴不等式的解集為![]() <x<
<x<![]()
∵![]()
![]() <
<![]() ,
,
∴不等式(2x-1)2<ax2的解集中整數解一定是1,2,3,
∴3<![]() ≤4,解得
≤4,解得![]() <a≤
<a≤![]() ,
,
∴a的取值范圍![]()


科目:高中數學 來源: 題型:
【題目】某校組織由5名學生參加的演講比賽,采用抽簽法決定演講順序,在“學生![]() 和
和![]() 都不是第一個出場,
都不是第一個出場,![]() 不是最后一個出場”的前提下,學生
不是最后一個出場”的前提下,學生![]() 第一個出場的概率為( )
第一個出場的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
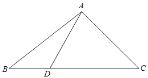
【題目】如圖所示,在△ABC中,D是BC邊上的一點,且AB=14,BD=6,∠ADC=![]() ,
,![]() .
.
(Ⅰ)求sin∠DAC;
(Ⅱ)求AD的長和△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知不等式![]() .
.
(1)若![]() 時,不等式恒成立,求實數m的取值范圍.
時,不等式恒成立,求實數m的取值范圍.
(2)若![]() 時不等式恒成立,求實數m的取值范圍.
時不等式恒成立,求實數m的取值范圍.
(3)若滿足![]() 的一切m的值使不等式恒成立,求實數x的取值范圍.
的一切m的值使不等式恒成立,求實數x的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,
(Ⅰ)若在函數![]() 的定義域內存在區間
的定義域內存在區間![]() ,使得該函數在區間
,使得該函數在區間![]() 上為減函數,求實數
上為減函數,求實數![]() 的取值范圍;
的取值范圍;
(Ⅱ)當![]() 時,若曲線
時,若曲線![]() 在點
在點![]() 處的切線
處的切線![]() 與曲線
與曲線![]() 有且只有一個公共點,求實數
有且只有一個公共點,求實數![]() 的值或取值范圍.
的值或取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年4月1日,新華通訊社發布:國務院決定設立河北雄安新區.消息一出,河北省雄縣、容城、安新3縣及周邊部分區域迅速成為海內外高度關注的焦點.
(1)為了響應國家號召,北京市某高校立即在所屬的8個學院的教職員工中作了“是否愿意將學校整體搬遷至雄安新區”的問卷調查,8個學院的調查人數及統計數據如下:
調查人數( | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
愿意整體搬遷人數( | 8 | 17 | 25 | 31 | 39 | 47 | 55 | 66 |
請根據上表提供的數據,用最小二乘法求出變量![]() 關于變量
關于變量![]() 的線性回歸方程
的線性回歸方程![]() 保留小數點后兩位有效數字);若該校共有教職員工2500人,請預測該校愿意將學校整體搬遷至雄安新區的人數;
保留小數點后兩位有效數字);若該校共有教職員工2500人,請預測該校愿意將學校整體搬遷至雄安新區的人數;
(2)若該校的8位院長中有5位院長愿意將學校整體搬遷至雄安新區,現該校擬在這8位院長中隨機選取4位院長組成考察團赴雄安新區進行實地考察,記![]() 為考察團中愿意將學校整體搬遷至雄安新區的院長人數,求
為考察團中愿意將學校整體搬遷至雄安新區的院長人數,求![]() 的分布列及數學期望.
的分布列及數學期望.
參考公式及數據:  .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一天,甲拿出一個裝有三張卡片的盒子(一張卡片的兩面都是綠色,一張卡片的兩面都是藍色,還有一張卡片一面是綠色,另一面是藍色),跟乙說玩一個游戲,規則是:甲將盒子里的卡片順序打亂后,由乙隨機抽出一張卡片放在桌子上,然后卡片朝下的面的顏色決定勝負,如果朝下的面的顏色與朝上的面的顏色一致,則甲贏,否則甲輸.乙對游戲的公平性提出了質疑,但是甲說:“當然公平!你看,如果朝上的面的顏色為綠色,則這張卡片不可能兩面都是藍色,因此朝下的面要么是綠色,要么是藍色,因此,你贏的概率為![]() ,我贏的概率也是
,我贏的概率也是![]() ,怎么不公平?”分析這個游戲是否公平.
,怎么不公平?”分析這個游戲是否公平.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com