
【題目】某公司過去五個月的廣告費支出x與銷售額y(單位:萬元)之間有下列對應數據:
x | 2 | 4 | 5 | 6 | 8 |
y |
| 40 | 60 | 50 | 70 |
工作人員不慎將表格中y的第一個數據丟失.已知y對x呈線性相關關系,且回歸方程為 ![]() =6.5x+17.5,則下列說法:
=6.5x+17.5,則下列說法:
①銷售額y與廣告費支出x正相關;
②丟失的數據(表中 ![]() 處)為30;
處)為30;
③該公司廣告費支出每增加1萬元,銷售額一定增加6.5萬元;
④若該公司下月廣告投入8萬元,則銷售額為70萬元.
其中,正確說法有( )
A.1個
B.2個
C.3個
D.4個
 全優點練單元計劃系列答案
全優點練單元計劃系列答案科目:高中數學 來源: 題型:
【題目】【2017安徽淮南二模】隨著社會發展,淮北市在一天的上下班時段也出現了堵車嚴重的現象.交通指數是交通擁堵指數的簡稱,是綜合反映道路網暢通或擁堵的概念.記交通指數為T,其范圍為[0,10],分別有5個級別:T∈[0,2)暢通;T∈[2,4)基本暢通;T∈[4,6)輕度擁堵;T∈[6,8)中度擁堵;T∈[8,10]嚴重擁堵.早高峰時段(T≥3 ),從淮北市交通指揮中心隨機選取了一至四馬路之間50個交通路段,依據交通指數數據繪制的直方圖如圖所示:
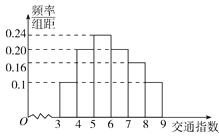
(I)據此直方圖估算交通指數T∈[4,8)時的中位數和平均數;
(II)據此直方圖求出早高峰一至四馬路之間的3個路段至少有2個嚴重擁堵的概率是多少?
(III)某人上班路上所用時間若暢通時為20分鐘,基本暢通為30分鐘,輕度擁堵為35分鐘,中度擁堵為45分鐘,嚴重擁堵為60分鐘,求此人用時間的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知直四棱柱ABCD﹣A1B1C1D1的底面ABCD為菱形,且∠BCD=60°,P為AD1的中點,Q為BC的中點 
(1)求證:PQ∥平面D1DCC1;
(2)求證:DQ⊥平面B1BCC1 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C的頂點在原點,焦點在x軸上,且拋物線上有一點P(4,m)到焦點的距離為6.
(Ⅰ)求拋物線C的方程;
(Ⅱ)若拋物線C與直線y=kx﹣2相交于不同的兩點A、B,且AB中點橫坐標為2,求k的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班同學準備參加學校在寒假里組織的“社區服務”、“進敬老院”、“參觀工廠”、“民俗調查”、“環保宣傳”五個項目的社會實踐活動,每天只安排一項活動,并要求在周一至周五內完成.其中“參觀工廠”與“環保宣講”兩項活動必須安排在相鄰兩天,“民俗調查”活動不能安排在周一.則不同安排方法的種數是( )
A.48 B.24 C.36 D.64
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數據x1 , x2 , x3 , …,x100是杭州市100個普通職工的2016年10月份的收入(均不超過2萬元),設這100個數據的中位數為x,平均數為y,方差為z,如果再加上馬云2016年10月份的收入x101(約100億元),則相對于x、y、z,這101個月收入數據( )
A.平均數可能不變,中位數可能不變,方差可能不變
B.平均數大大增大,中位數可能不變,方差也不變
C.平均數大大增大,中位數一定變大,方差可能不變
D.平均數大大增大,中位數可能不變,方差變大
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某制造廠商10月份生產了一批乒乓球,從中隨機抽取n個進行檢查,測得每個球的直徑(單位:mm),將數據進行分組,得到如表頻率分布表:
分組 | 頻數 | 頻率 |
[39.95,39.97) | 6 | P1 |
[39.97,39.99) | 12 | 0.20 |
[39.99,40.01) | a | 0.50 |
[40.01,40.03) | b | P2 |
合計 | n | 1.00 |
(1)求a、b、n及P1、P2的值,并畫出頻率分布直方圖(結果保留兩位小數); 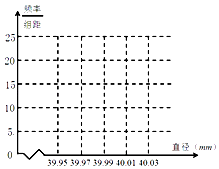
(2)已知標準乒乓球的直徑為40.00mm,直徑誤差不超過0.01mm的為五星乒乓球,若這批乒乓球共有10000個,試估計其中五星乒乓球的數目;
(3)統計方法中,同一組數據常用該組區間的中點值(例如區間[39.99,40.01)的中點值是40.00)作為代表,估計這批乒乓球直徑的平均值和中位數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l:y=2x+m與圓O:x2+y2=1相交于A,B兩個不同的點,且A(cosα,sinα),B(cosβ,sinβ).
(1)當△AOB面積最大時,求m的取值,并求出|AB|的長度.
(2)判斷sin(α+β)是否為定值;若是,求出定值的大小;若不是,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Sn , 且滿足an+2SnSn﹣1=0(n≥2),a1= ![]() .
.
(1)求證:{ ![]() }是等差數列;
}是等差數列;
(2)求an的表達式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com