
【題目】某校高一(1)班的一次數學測試成績的莖葉圖和頻率分布直方圖都受到不同程度的污損,可見部分如下圖.

(1)求分數在![]() 的頻率及全班人數;
的頻率及全班人數;
(2)求分數在![]() 之間的頻數,并計算頻率分布直方圖中
之間的頻數,并計算頻率分布直方圖中![]() 間矩形的高;
間矩形的高;
(3)若要從分數在![]() 之間的試卷中任取兩份分析學生失分情況,求在抽取的試卷中,至少有一份分數在
之間的試卷中任取兩份分析學生失分情況,求在抽取的試卷中,至少有一份分數在![]() 之間的概率.
之間的概率.
【答案】(1)頻率為![]() ,全班人數為
,全班人數為![]() ;(2)頻數為
;(2)頻數為![]() ,矩形的高為
,矩形的高為![]() ;(3)
;(3)![]() .
.
【解析】
試題分析:(1)分數在![]() 的頻率為第一組矩形的面積,全班人數為該組的頻數與頻率的比值;(2)用全班人數送去其余組的人數為
的頻率為第一組矩形的面積,全班人數為該組的頻數與頻率的比值;(2)用全班人數送去其余組的人數為![]() 之間的頻數,用該組的頻率與組距的組距的比值為矩形的高;(3)首先用列舉法列舉出所有的基本事件,然后找出符合題意的基本事件個數,從而利用古典概型概率公式計算即可.
之間的頻數,用該組的頻率與組距的組距的比值為矩形的高;(3)首先用列舉法列舉出所有的基本事件,然后找出符合題意的基本事件個數,從而利用古典概型概率公式計算即可.
試題解析:(1)分數在![]() 的頻率為
的頻率為![]() ,
,
由莖葉圖知:分數在![]() 之間的頻數為2,所以全班人數為
之間的頻數為2,所以全班人數為![]() .
.
(2)分數在![]() 之間的頻數為
之間的頻數為![]() ;
;
頻率分布直方圖中![]() 間的矩形的高為
間的矩形的高為![]() .
.
(3)將![]() 之間的3個分數編號為
之間的3個分數編號為![]() ,
,![]() 之間的2個分數編號為
之間的2個分數編號為![]() ,
,
在![]() 之間的試卷中任取兩份的基本事件為:
之間的試卷中任取兩份的基本事件為:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共10個,
共10個,
其中,至少有一個在![]() 之間的基本事件有7個,
之間的基本事件有7個,
故至少有一份分數在![]() 之間的概率是
之間的概率是![]() .
.


科目:高中數學 來源: 題型:
【題目】為了了解某省各景點在大眾中的熟知度,隨機對15~65歲的人群抽樣了![]() 人,回答問題“某省有哪幾個著名的旅游景點?”統計結果如下圖表
人,回答問題“某省有哪幾個著名的旅游景點?”統計結果如下圖表
組號 | 分組 | 回答正確 的人數 | 回答正確的人數 占本組的頻率 |
第1組 | [15,25) |
| 0.5 |
第2組 | [25,35) | 18 |
|
第3組 | [35,45) |
| 0.9 |
第4組 | [45,55) | 9 | 0.36 |
第5組 | [55,65] | 3 |
|

(1)分別求出![]() 的值;
的值;
(2)從第2,3,4組回答正確的人中用分層抽樣的方法抽取6人,求第2,3,4組每組各抽取多少人?
(3)在(2)抽取的6人中隨機抽取2人,求所抽取的人中恰好沒有第3組人的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在育民中學舉行的電腦知識競賽中,將九年級兩個班參賽的學生成績(得分均為整數)進行整理后分成五組,繪制如圖所示的頻率分布直方圖.已知圖中從左到右的第一、第三、第四、第五小組的頻率分別是0.30,0.15,0.10,0.05,第二小組的頻數是40.

(1)求第二小組的頻率,并補全這個頻率分布直方圖;
(2)求這兩個班參賽的學生人數是多少;
(3)這兩個班參賽學生的成績的中位數應落在第幾小組內.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的焦點在原點
的焦點在原點![]() ,左焦點
,左焦點![]() ,左頂點
,左頂點![]() ,上頂點
,上頂點![]() ,
,![]() 的周長為
的周長為![]() ,
,![]() 的面積為
的面積為![]() .
.
(I)求橢圓![]() 的標準方程;
的標準方程;
(II)是否存在與橢圓![]() 交于
交于![]() 兩點的直線
兩點的直線![]() 使得
使得![]() 成立?若存在,求出實數
成立?若存在,求出實數![]() 的取值范圍,若不存在,說明理由.
的取值范圍,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了豐富高學生的課外生活,某校要組建數學計算機航空模型3個興趣小組,小明要選報其中的2個,則包含的樣本點共有( )
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,且曲線
,且曲線![]() 的左焦點
的左焦點![]() 在直線
在直線![]() 上.
上.
(1)若直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值;
的值;
(2)求曲線![]() 的內接矩形的周長的最大值.
的內接矩形的周長的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形ABCD為正方形,PD⊥平面ABCD,PD∥QA,QA=AB=![]() PD.
PD.
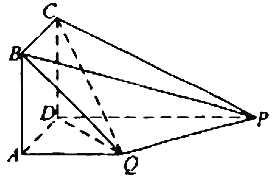
(I)證明:平面PQC⊥平面DCQ
(II)求二面角Q-BP-C的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com