
【題目】已知函數(shù)![]() .
.
(1)求函數(shù)![]() 的圖象在
的圖象在![]() 處的切線方程;
處的切線方程;
(2)若任意![]() ,不等式
,不等式![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(3)設(shè)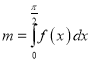 ,
, ![]() ,證明:
,證明: ![]() .
.
【答案】(1)![]() (2)
(2) ![]() (3)見(jiàn)解析
(3)見(jiàn)解析
【解析】試題分析:(1)本問(wèn)考查導(dǎo)數(shù)的幾何意義, ![]() ,
, ![]() ,于是可得切線方程為
,于是可得切線方程為![]() ;(2)本問(wèn)考查利用導(dǎo)數(shù)研究恒成立問(wèn)題,不等式
;(2)本問(wèn)考查利用導(dǎo)數(shù)研究恒成立問(wèn)題,不等式![]() 恒成立
恒成立![]() ,設(shè)函數(shù)
,設(shè)函數(shù)![]() ,則轉(zhuǎn)化為當(dāng)
,則轉(zhuǎn)化為當(dāng)![]() 時(shí),
時(shí), ![]() 恒成立,對(duì)函數(shù)
恒成立,對(duì)函數(shù)![]() 求導(dǎo),
求導(dǎo), ![]() ,再令
,再令![]() ,對(duì)
,對(duì)![]() 求導(dǎo),
求導(dǎo), ![]() ,通過(guò)對(duì)
,通過(guò)對(duì)![]() 分區(qū)間討論,使得
分區(qū)間討論,使得![]() 恒成立,從而得到
恒成立,從而得到![]() 的取值范圍;(3)首先通過(guò)微積分定理求出
的取值范圍;(3)首先通過(guò)微積分定理求出![]() ,則
,則![]() ,由(2)知,當(dāng)
,由(2)知,當(dāng)![]() 時(shí),
時(shí), ![]() ,即
,即![]() ,構(gòu)造函數(shù)
,構(gòu)造函數(shù)![]() ,通過(guò)證明該函數(shù)的單調(diào)性,易得出
,通過(guò)證明該函數(shù)的單調(diào)性,易得出![]() 在
在![]() 上恒成立,令
上恒成立,令![]() ,于是通過(guò)不等式的放縮,可以得到待證明的結(jié)論.
,于是通過(guò)不等式的放縮,可以得到待證明的結(jié)論.
試題解析:(1)![]() ,
, ![]() ,∴切線為
,∴切線為![]()
(2)![]()
![]() ,令
,令![]()
則![]()
又令![]()
![]()
①當(dāng)![]() ,即
,即![]() 時(shí),
時(shí), ![]() 恒成立,∴
恒成立,∴![]() 遞增
遞增
∴![]() ,∴
,∴![]() ,∴
,∴![]() 遞增
遞增
∴![]() (不合題意)
(不合題意)
②當(dāng)![]() 即
即![]() 時(shí),
時(shí), ![]()
![]() 遞減,
遞減,
∴![]() ,∴
,∴![]() ,∴
,∴![]() 遞減
遞減
∴![]() (符合題意)
(符合題意)
③當(dāng)![]() ,即
,即![]() 時(shí),由
時(shí),由![]()
![]() ,∴在
,∴在![]() 上,
上, ![]() ,使
,使![]()
且![]() 時(shí),
時(shí), ![]() ,∴
,∴![]() 遞增,∴
遞增,∴![]() (不符合題意)
(不符合題意)
綜上: ![]() .
.
(3)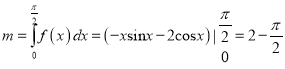
∴![]() ,由(2)知,當(dāng)
,由(2)知,當(dāng)![]() 時(shí),
時(shí), ![]() ,∴
,∴![]() ,
,
又令![]() ,
, ![]()
![]() ,∴
,∴![]() 遞減
遞減
![]() 即
即![]() 在
在![]() 上恒成立,令
上恒成立,令![]()
∴原不等式![]()
∴左式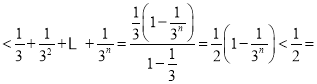 右式
右式
∴得證.


 智能訓(xùn)練練測(cè)考系列答案
智能訓(xùn)練練測(cè)考系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】(本小題滿分12分) 某中學(xué)的環(huán)保社團(tuán)參照國(guó)家環(huán)境標(biāo)準(zhǔn)制定了該校所在區(qū)域空氣質(zhì)量指數(shù)與空氣質(zhì)量等級(jí)對(duì)應(yīng)關(guān)系如下表(假設(shè)該區(qū)域空氣質(zhì)量指數(shù)不會(huì)超過(guò)![]() ):
):
空氣質(zhì)量指數(shù) |
|
|
|
|
|
|
空氣質(zhì)量等級(jí) |
|
|
|
|
|
|
該社團(tuán)將該校區(qū)在![]() 年
年![]() 天的空氣質(zhì)量指數(shù)監(jiān)測(cè)數(shù)據(jù)作為樣本,繪制的頻率分布直方圖如下圖,把該直方圖所得頻率估計(jì)為概率.
天的空氣質(zhì)量指數(shù)監(jiān)測(cè)數(shù)據(jù)作為樣本,繪制的頻率分布直方圖如下圖,把該直方圖所得頻率估計(jì)為概率.
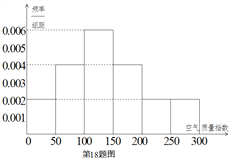
(Ⅰ)請(qǐng)估算![]() 年(以
年(以![]() 天計(jì)算)全年空氣質(zhì)量?jī)?yōu)良的天數(shù)(未滿一天按一天計(jì)算);
天計(jì)算)全年空氣質(zhì)量?jī)?yōu)良的天數(shù)(未滿一天按一天計(jì)算);
(Ⅱ)該校![]() 年
年![]() 月
月![]() 、
、![]() 日將作為高考考場(chǎng),若這兩天中某天出現(xiàn)
日將作為高考考場(chǎng),若這兩天中某天出現(xiàn)![]() 級(jí)重度污染,需要凈化空氣費(fèi)用
級(jí)重度污染,需要凈化空氣費(fèi)用![]() 元,出現(xiàn)
元,出現(xiàn)![]() 級(jí)嚴(yán)重污染,需要凈化空氣費(fèi)用
級(jí)嚴(yán)重污染,需要凈化空氣費(fèi)用![]() 元,記這兩天凈化空氣總費(fèi)用為
元,記這兩天凈化空氣總費(fèi)用為![]() 元,求
元,求![]() 的分布列及數(shù)學(xué)期望.
的分布列及數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
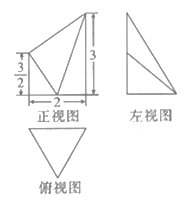
【題目】如圖,某幾何體的三視圖中,俯視圖是邊長(zhǎng)為2的正三角形,正視圖和左視圖分別為直角梯形和直角三角形,則該幾何體的體積為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知數(shù)列{an}的通項(xiàng)公式為an= ![]() ﹣n.
﹣n.
(1)證明:數(shù)列{an}是等差數(shù)列;
(2)求此數(shù)列的前二十項(xiàng)和S20 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知拋物線x2=y+1上一定點(diǎn)A(﹣1,0)和兩動(dòng)點(diǎn)P,Q,當(dāng)PA⊥PQ時(shí),點(diǎn)Q的橫坐標(biāo)的取值范圍是( )
A.(﹣∞,﹣3]
B.[1,+∞)
C.[﹣3,1]
D.(﹣∞,﹣3]∪[1,+∞)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,設(shè)不等式組 ![]() 所表示的平面區(qū)域是W,從區(qū)域W中隨機(jī)取點(diǎn)M(x,y).
所表示的平面區(qū)域是W,從區(qū)域W中隨機(jī)取點(diǎn)M(x,y).
(1)若x,y∈Z,求點(diǎn)M位于第一象限的概率;
(2)若x,y∈R,求|OM|≥1的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
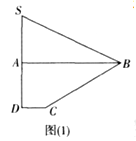
【題目】如圖(1)所示,已知四邊形![]() 是由直角△
是由直角△![]() 和直角梯形
和直角梯形![]() 拼接而成的,其中
拼接而成的,其中![]()
![]() .且點(diǎn)
.且點(diǎn)![]() 為線段
為線段![]() 的中點(diǎn),
的中點(diǎn), ![]() ,
, ![]() 現(xiàn)將△
現(xiàn)將△![]() 沿
沿![]() 進(jìn)行翻折,使得二面角
進(jìn)行翻折,使得二面角![]()
![]() 的大小為
的大小為![]() ,得到圖形如圖(2)所示,連接
,得到圖形如圖(2)所示,連接![]() ,點(diǎn)
,點(diǎn)![]() 分別在線段
分別在線段![]() 上.
上.
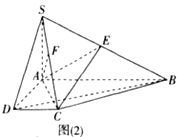
(1)證明: ![]() ;
;
(2)若三棱錐![]() 的體積為四棱錐
的體積為四棱錐![]() 體積的
體積的![]() ,求點(diǎn)
,求點(diǎn)![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某同學(xué)用“五點(diǎn)法”畫(huà)函數(shù)f(x)=Asin(ωx+φ)(ω>0,|φ|< ![]() )在某一個(gè)周期內(nèi)的圖象時(shí),列表并填入的部分?jǐn)?shù)據(jù)如表:
)在某一個(gè)周期內(nèi)的圖象時(shí),列表并填入的部分?jǐn)?shù)據(jù)如表:
x |
|
| |||
ωx+φ | 0 |
| π |
| 2π |
Asin(ωx+φ) | 0 | 2 | 0 | ﹣2 |
(1)請(qǐng)將上表數(shù)據(jù)補(bǔ)全,并直接寫(xiě)出函數(shù)f(x)的解析式;
(2)當(dāng)x∈[0, ![]() ]時(shí),求函數(shù)f(x)的值域.
]時(shí),求函數(shù)f(x)的值域.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() 是自然對(duì)數(shù)的底數(shù)).
是自然對(duì)數(shù)的底數(shù)).
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若![]() ,當(dāng)
,當(dāng)![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 的最大值;
的最大值;
(3)若![]() 且
且![]() ,求證:
,求證: ![]() .
.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com