
【題目】某山區(qū)外圍有兩條相互垂直的直線型公路,為進(jìn)一步改善山區(qū)的交通現(xiàn)狀,計劃修建一條連接兩條公路和山區(qū)邊界的直線型公路.記兩條相互垂直的公路為![]() ,山區(qū)邊界曲線為
,山區(qū)邊界曲線為![]() .計劃修建的公路為
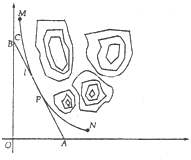
.計劃修建的公路為![]() ,如圖所示,
,如圖所示,![]() 為
為![]() 的兩個端點,測得點
的兩個端點,測得點![]() 到
到![]() 的距離分別為5千米和40千米,點
的距離分別為5千米和40千米,點![]() 到
到![]() 的距離分別為20千米和2.5千米,以
的距離分別為20千米和2.5千米,以![]() 所在直線分別為
所在直線分別為![]() 軸,建立平面直角坐標(biāo)系
軸,建立平面直角坐標(biāo)系![]() .假設(shè)曲線
.假設(shè)曲線![]() 符合函數(shù)
符合函數(shù)![]() (其中
(其中![]() 為常數(shù))模型.
為常數(shù))模型.
(1)求![]() 的值;
的值;
(2)設(shè)公路![]() 與曲線
與曲線![]() 相切于
相切于![]() 點,
點,![]() 的橫坐標(biāo)為
的橫坐標(biāo)為![]() .
.
①請寫出公路![]() 長度的函數(shù)解析式
長度的函數(shù)解析式![]() ,并寫出其定義域;
,并寫出其定義域;
②當(dāng)![]() 為何值時,公路
為何值時,公路![]() 的長度最短?求出最短長度.
的長度最短?求出最短長度.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②當(dāng)
;②當(dāng)![]() 時,公路
時,公路![]() 的長度最短,最短長度為
的長度最短,最短長度為![]() 千米.
千米.
【解析】
試題分析:(1)由題意得![]() 分別為
分別為 ![]()
![]()
![]()
![]()

![]()
![]() ;(2)①由(1)知
;(2)①由(1)知![]()
![]()
![]()
![]() ,求導(dǎo)得
,求導(dǎo)得![]()
![]()
![]() ;
;![]()
![]()
![]()
![]()
![]() ;
;
②設(shè)![]()
![]()
![]() ,令
,令![]()
![]()
![]() ,利用導(dǎo)數(shù)工具可得:當(dāng)
,利用導(dǎo)數(shù)工具可得:當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 有極小值,也是最小值,所以
有極小值,也是最小值,所以![]() ,此時
,此時![]() .
.
試題解析:
(1)由題意知,點![]() 的坐標(biāo)分別為
的坐標(biāo)分別為![]() .
.
將其分別代入![]() ,得
,得 ,解得
,解得![]() .
.
(2)①由(1)知,![]() ,則點
,則點![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,
,
設(shè)在點![]() 處的切線
處的切線![]() 交
交![]() 軸分別交于
軸分別交于![]() 點,
點,![]() ,
,
則![]() 的方程為
的方程為![]() ,由此得
,由此得![]() .
.
故
②設(shè)![]() ,則
,則![]() ,令
,令![]() ,解得
,解得![]() .
.
當(dāng)![]() 時,
時,![]() ,
,![]() 是減函數(shù);
是減函數(shù);
當(dāng)![]() 時,
時,![]() 是增函數(shù).
是增函數(shù).
從而,當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 有極小值,也是最小值,所以
有極小值,也是最小值,所以![]() ,
,
此時![]() ,
,
答:當(dāng)![]() 時,公路
時,公路![]() 的長度最短,最短長度為
的長度最短,最短長度為![]() 千米
千米


科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了解某校學(xué)生的視力情況,現(xiàn)采用隨機(jī)抽樣的方式從該校的![]() 兩班中各抽5名學(xué)生進(jìn)行視力檢測,檢測的數(shù)據(jù)如下:
兩班中各抽5名學(xué)生進(jìn)行視力檢測,檢測的數(shù)據(jù)如下:
![]() 班5名學(xué)生的視力檢測結(jié)果是:
班5名學(xué)生的視力檢測結(jié)果是:![]() .
.
![]() 班5名學(xué)生的視力檢測結(jié)果是:
班5名學(xué)生的視力檢測結(jié)果是:![]() .
.
(1)分別計算兩組數(shù)據(jù)的平均數(shù),從計算結(jié)果看,哪個班的學(xué)生視力較好?并計算![]() 班的5名學(xué)生視力的方差;
班的5名學(xué)生視力的方差;
(2)現(xiàn)從![]() 班上述5名學(xué)生中隨機(jī)選取2名,求這2名學(xué)生中至少有1名學(xué)生的視力低于
班上述5名學(xué)生中隨機(jī)選取2名,求這2名學(xué)生中至少有1名學(xué)生的視力低于![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了解今年某校高三畢業(yè)班想?yún)④姷膶W(xué)生體重情況,將所得的數(shù)據(jù)整理后,畫出了頻率分布直方圖(如圖).已知圖中從左到右的前3個小組的頻率之比為1:2:3,其中第2小組的頻數(shù)為24.
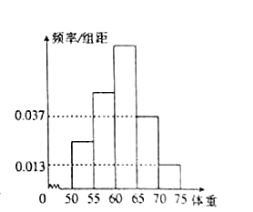
(Ⅰ)求該校高三畢業(yè)班想?yún)④姷膶W(xué)生人數(shù);
(Ⅱ)以這所學(xué)校的樣本數(shù)據(jù)來估計全省的總體數(shù)據(jù),若從全省高三畢業(yè)班想?yún)④姷耐瑢W(xué)中(人數(shù)很多)任選三人,設(shè)![]() 表示體重超過60公斤的學(xué)生人數(shù),求
表示體重超過60公斤的學(xué)生人數(shù),求![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】連江一中第49屆田徑運(yùn)動會提出了“我運(yùn)動、我陽光、我健康、我快樂”的口號,某同學(xué)要設(shè)計一張如圖所示的豎向張貼的長方形海報進(jìn)行宣傳,要求版心面積為162 ![]() (版心是指圖中的長方形陰影部分,
(版心是指圖中的長方形陰影部分,![]() 為長度單位分米),上、下兩邊各空2
為長度單位分米),上、下兩邊各空2 ![]() ,左、右兩邊各空1
,左、右兩邊各空1 ![]() .
.

(Ⅰ)若設(shè)版心的高為![]()
![]() ,求海報四周空白面積關(guān)于
,求海報四周空白面積關(guān)于![]() 的函數(shù)
的函數(shù)![]() 的解析式;
的解析式;
(Ⅱ)要使海報四周空白面積最小,版心的高和寬該如何設(shè)計?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f (x)=lg(ax2+2x+1) .
(1)若函數(shù)f (x)的定義域為R,求實數(shù)a的取值范圍;
(2)若函數(shù)f (x)的值域為R,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
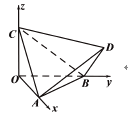
【題目】如圖,正四面體![]() 的頂點
的頂點![]() 、
、![]() 、
、![]() 分別在兩兩垂直的三條射線
分別在兩兩垂直的三條射線![]() ,
, ![]() ,
, ![]() 上,則在下列命題中,錯誤的是( )
上,則在下列命題中,錯誤的是( )
A. ![]() 是正三棱錐
是正三棱錐
B. 直線![]() 與平面
與平面![]() 相交
相交
C. 直線![]() 與平面
與平面![]() 所成的角的正弦值為
所成的角的正弦值為![]()
D. 異面直線![]() 和
和![]() 所成角是
所成角是![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】迭代法是用于求方程或方程組近似根的一種常用的算法設(shè)計方法.設(shè)方程為![]() ,用某種數(shù)學(xué)方法到處等價的形式
,用某種數(shù)學(xué)方法到處等價的形式![]() ,然后按以下步驟執(zhí)行:
,然后按以下步驟執(zhí)行:
(1)選一個方程的近似根,賦給變量![]() ;
;
(2)將![]() 的值保存于變量
的值保存于變量![]() ,然后計算
,然后計算![]() ,并將結(jié)果存于變量
,并將結(jié)果存于變量![]() ;
;
(3)當(dāng)![]() 與
與![]() 的差的絕對值還小于指定的精度要求時,重復(fù)步驟(2)的計算.若方程有根,則按上述方法求得的
的差的絕對值還小于指定的精度要求時,重復(fù)步驟(2)的計算.若方程有根,則按上述方法求得的![]() 就認(rèn)為是方程的根.試用迭代法求某個數(shù)的平方根,用流程圖和偽代碼表示問題的算法.
就認(rèn)為是方程的根.試用迭代法求某個數(shù)的平方根,用流程圖和偽代碼表示問題的算法.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com