
【題目】為了了解某工廠開展群眾體育活動的情況,擬采用分層抽樣的方法從A,B,C三個區(qū)中抽取7個工廠進行調(diào)查,已知A,B,C區(qū)中分別有18,27,18個工廠
(Ⅰ)求從A,B,C區(qū)中分別抽取的工廠個數(shù);
(Ⅱ)若從抽取的7個工廠中隨機抽取2個進行調(diào)查結(jié)果的對比,求這2個工廠中至少有1個來自A區(qū)的概率。
【答案】(1) 2,3,2;(2) ![]() .
.
【解析】本試題主要考查了統(tǒng)計和概率的綜合運用。
第一問工廠總數(shù)為18+27+18=63,樣本容量與總體中的個體數(shù)比為7/63=1/9…3分
所以從A,B,C三個區(qū)中應(yīng)分別抽取的工廠個數(shù)為2,3,2。
第二問設(shè)A1,A2為在A區(qū)中的抽得的2個工廠,B1,B2,B3為在B區(qū)中抽得的3個工廠,
C1,C2為在C區(qū)中抽得的2個工廠。
這7個工廠中隨機的抽取2個,全部的可能結(jié)果有1/2*7*6=32種。
隨機的抽取的2個工廠至少有一個來自A區(qū)的結(jié)果有A1,A2),A1,B2),A1,B1),
A1,B3)A1,C2),A1,C1), …………9分
同理A2還能給合5種,一共有11種。
所以所求的概率為p=11/21


 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)設(shè)![]() ,將函數(shù)
,將函數(shù)![]() 表示為關(guān)于
表示為關(guān)于![]() 的函數(shù)
的函數(shù)![]() ,求
,求![]() 的解析式;
的解析式;
(2)對任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列說法中錯誤的是( )
A.在三角形中,已知兩邊及其一邊的對角,不能用余弦定理求解三角形
B.余弦定理揭示了任意三角形邊角之間的關(guān)系,因此它適用于任何三角形
C.利用余弦定理,可以解決已知三角形三邊求角的問題
D.在三角形中,勾股定理是余弦定理的特例
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某地政府為科技興市,欲將如圖所示的一塊不規(guī)則的非農(nóng)業(yè)用地規(guī)劃建成一個矩形的高科技工業(yè)園區(qū).已知![]() ,
,![]() ,
,![]() ,曲線
,曲線![]() 是以點
是以點![]() 為頂點的且開口向上的拋物線的一段,如果要使矩形的相鄰兩邊分別落在
為頂點的且開口向上的拋物線的一段,如果要使矩形的相鄰兩邊分別落在![]() ,
,![]() 上,且一個頂點落在曲線段
上,且一個頂點落在曲線段![]() 上,問矩形的兩邊長分別為多少時使矩形工業(yè)園區(qū)的用地面積最大?
上,問矩形的兩邊長分別為多少時使矩形工業(yè)園區(qū)的用地面積最大?

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖所示,在三棱錐A-BOC中,OA⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,BC=![]() ,動點D在線段AB上.
,動點D在線段AB上.
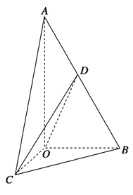
(1)求證:平面COD⊥平面AOB;
(2)當OD⊥AB時,求三棱錐C-OBD的體積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖所示,在△ABC中,a=b·cos C+c·cos B,其中a,b,c分別為角A,B,C的對邊,在四面體PABC中,S1,S2,S3,S分別表示△PAB,△PBC,△PCA,△ABC的面積,α,β,γ依次表示面PAB,面PBC,面PCA與底面ABC所成二面角的大小.寫出對四面體性質(zhì)的猜想,并證明你的結(jié)論


查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)有以下四個命題:
①底面是平行四邊形的四棱柱是平行六面體;
②底面是矩形的平行六面體是長方體;
③直四棱柱是直平行六面體;
④棱臺的相對側(cè)棱延長后必交于一點.
其中正確命題的序號是______.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】春節(jié)期間某超市搞促銷活動,當顧客購買商品的金額達到一定數(shù)量后可以參加抽獎活動,活動規(guī)則為:從裝有![]() 個黑球,
個黑球, ![]() 個紅球,
個紅球, ![]() 個白球的箱子中(除顏色外,球完全相同)摸球.
個白球的箱子中(除顏色外,球完全相同)摸球.
(Ⅰ)當顧客購買金額超過![]() 元而不超過
元而不超過![]() 元時,可從箱子中一次性摸出
元時,可從箱子中一次性摸出![]() 個小球,每摸出一個黑球獎勵
個小球,每摸出一個黑球獎勵![]() 元的現(xiàn)金,每摸出一個紅球獎勵
元的現(xiàn)金,每摸出一個紅球獎勵![]() 元的現(xiàn)金,每摸出一個白球獎勵
元的現(xiàn)金,每摸出一個白球獎勵![]() 元的現(xiàn)金,求獎金數(shù)不少于
元的現(xiàn)金,求獎金數(shù)不少于![]() 元的概率;
元的概率;
(Ⅱ)當購買金額超過![]() 元時,可從箱子中摸兩次,每次摸出
元時,可從箱子中摸兩次,每次摸出![]() 個小球后,放回再摸一次,每摸出一個黑球和白球一樣獎勵
個小球后,放回再摸一次,每摸出一個黑球和白球一樣獎勵![]() 元的現(xiàn)金,每摸出一個紅球獎勵
元的現(xiàn)金,每摸出一個紅球獎勵![]() 元的現(xiàn)金,求獎金數(shù)小于
元的現(xiàn)金,求獎金數(shù)小于![]() 元的概率.
元的概率.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com