
已知橢圓![]() 的離心率為
的離心率為![]() ,F(xiàn)為橢圓在x軸正半軸上的焦點(diǎn),M、N兩點(diǎn)在橢圓C上,且
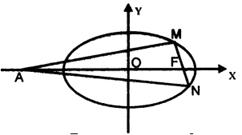
,F(xiàn)為橢圓在x軸正半軸上的焦點(diǎn),M、N兩點(diǎn)在橢圓C上,且![]() ,定點(diǎn)A(-4,0).
,定點(diǎn)A(-4,0).
(1)求證:當(dāng)![]() 時(shí).,
時(shí).,![]() ;
;
(2)若當(dāng)![]() 時(shí)有
時(shí)有![]() ,求橢圓C的方程;
,求橢圓C的方程;
(3)在(2)的條件下,當(dāng)M、N兩點(diǎn)在橢圓C運(yùn)動時(shí),當(dāng)![]() 的值為6
的值為6![]() 時(shí), 求出直線MN的方程.
時(shí), 求出直線MN的方程.
(1)見解析
(2)橢圓C的方程為![]()
(3)直線的MN方程為![]() ,或
,或![]() 。
。
(1)設(shè)![]() ,
,
則![]() ,
,
當(dāng)![]() 時(shí),
時(shí),![]() ,
,
由M,N兩點(diǎn)在橢圓上,![]()
若![]() ,則
,則![]() (舍去),
(舍去),![]() (4分)
(4分)
![]() 。(5分)
。(5分)
(2)當(dāng)![]() 時(shí),不妨設(shè)
時(shí),不妨設(shè)![]() (6分)
(6分)
又![]() ,
,![]() , (8分)
, (8分)
橢圓C的方程為![]() 。 (9分)
。 (9分)
(3)因?yàn)?img width=327 height=28 src="http://thumb.zyjl.cn/pic1/1899/sx/80/243680.gif">=6![]() , (10分)
, (10分)
由(2)知點(diǎn)F(2,0), 所以|AF|=6, 即得|yM-yN|=![]() (11分)
(11分)
當(dāng)MN⊥x軸時(shí), |yM-yN|=|MN|=![]() , 故直線MN的斜率存在, (12分)
, 故直線MN的斜率存在, (12分)
不妨設(shè)直線MN的方程為![]()
聯(lián)立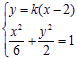 ,得
,得![]() ,
,
![]() =
=![]() , 解得k=±1。
, 解得k=±1。
此時(shí),直線的MN方程為![]() ,或
,或![]() 。 (14分)
。 (14分)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上均不對 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 如圖,在由圓O:x2+y2=1和橢圓C:
如圖,在由圓O:x2+y2=1和橢圓C:| x2 |
| a2 |
| ||
| 3 |
| OA |
| OB |
| 1 |
| 2 |
| OM |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| ||
| 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 如圖,A,B是橢圓C:
如圖,A,B是橢圓C:| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com