
【題目】已知函數(shù)f(x)=xlnx,g(x)=﹣x2+ax﹣3.
(1)求函數(shù)f(x)在[t,t+2](t>0)上的最小值;
(2)若存在x0∈[ ![]() ,e](e是自然對(duì)數(shù)的底數(shù),e=2.71828…),使不等式2f(x0)≥g(x0)成立,求實(shí)數(shù)a的取值范圍.
,e](e是自然對(duì)數(shù)的底數(shù),e=2.71828…),使不等式2f(x0)≥g(x0)成立,求實(shí)數(shù)a的取值范圍.
【答案】
(1)解:由已知知函數(shù)f(x)的定義域?yàn)椋?,+∞),f′(x)=lnx+1,
當(dāng)x∈(0, ![]() ),f′(x)<0,f(x)單調(diào)遞減,
),f′(x)<0,f(x)單調(diào)遞減,
當(dāng)x∈( ![]() ),f′(x)>0,f(x)單調(diào)遞增,
),f′(x)>0,f(x)單調(diào)遞增,
∵t>0,∴t+2> ![]()
② 當(dāng)0<t< ![]() <t+2,即0<t<
<t+2,即0<t< ![]() 時(shí),f(x)min=f(
時(shí),f(x)min=f( ![]() )=﹣
)=﹣ ![]() ;
;
②當(dāng) ![]() ,即t
,即t ![]() 時(shí),f(x)在[t,t+2]上單調(diào)遞增,f(x)min=f(t)=tlnt.
時(shí),f(x)在[t,t+2]上單調(diào)遞增,f(x)min=f(t)=tlnt.
∴  .
.
(2)解:∵不等式2f(x0)≥g(x0)成立,即2x0lnx0≥﹣ ![]() ,
,
∴a≤2lnx+x+ ![]() ,x∈[
,x∈[ ![]() ,e],
,e],
設(shè)h(x)=2lnx+x+ ![]() ,x∈[
,x∈[ ![]() ,e],
,e],
則 ![]() ,x∈[
,x∈[ ![]() ,e],
,e],
①x∈[ ![]() ,1)時(shí),h′(x)<0,h(x)單調(diào)遞減,
,1)時(shí),h′(x)<0,h(x)單調(diào)遞減,
②x∈(1,e]時(shí),h′(x)>0,h(x)單調(diào)遞增,
∴h(x)max=h( ![]() )=﹣2+
)=﹣2+ ![]() ,對(duì)一切x0∈[
,對(duì)一切x0∈[ ![]() ,e]使不等式2f(x0)≥g(x0)成立,
,e]使不等式2f(x0)≥g(x0)成立,
∴a≤h(x)max=﹣2+ ![]() +3e.
+3e.
【解析】(1)由已知知函數(shù)f(x)的定義域?yàn)椋?,+∞),f′(x)=lnx+1,由此利用導(dǎo)數(shù)性質(zhì)能求出函數(shù)f(x)在[t,t+2](t>0)上的最小值.(2)由已知得a≤2lnx+x+ ![]() ,x∈[
,x∈[ ![]() ,e],設(shè)h(x)=2lnx+x+
,e],設(shè)h(x)=2lnx+x+ ![]() ,x∈[
,x∈[ ![]() ,e],則
,e],則 ![]() ,x∈[
,x∈[ ![]() ,e],由此利用導(dǎo)數(shù)性質(zhì)能求出實(shí)數(shù)a的取值
,e],由此利用導(dǎo)數(shù)性質(zhì)能求出實(shí)數(shù)a的取值
【考點(diǎn)精析】掌握利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性和函數(shù)的最大(小)值與導(dǎo)數(shù)是解答本題的根本,需要知道一般的,函數(shù)的單調(diào)性與其導(dǎo)數(shù)的正負(fù)有如下關(guān)系: 在某個(gè)區(qū)間![]() 內(nèi),(1)如果
內(nèi),(1)如果![]() ,那么函數(shù)
,那么函數(shù)![]() 在這個(gè)區(qū)間單調(diào)遞增;(2)如果
在這個(gè)區(qū)間單調(diào)遞增;(2)如果![]() ,那么函數(shù)
,那么函數(shù)![]() 在這個(gè)區(qū)間單調(diào)遞減;求函數(shù)
在這個(gè)區(qū)間單調(diào)遞減;求函數(shù)![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數(shù)
上的最大值與最小值的步驟:(1)求函數(shù)![]() 在
在![]() 內(nèi)的極值;(2)將函數(shù)
內(nèi)的極值;(2)將函數(shù)![]() 的各極值與端點(diǎn)處的函數(shù)值
的各極值與端點(diǎn)處的函數(shù)值![]() ,
,![]() 比較,其中最大的是一個(gè)最大值,最小的是最小值.
比較,其中最大的是一個(gè)最大值,最小的是最小值.


 浙江名校名師金卷系列答案
浙江名校名師金卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在△ABC中,M是邊BC的中點(diǎn),tan∠BAM= ![]() ,cos∠AMC=﹣
,cos∠AMC=﹣ ![]() (Ⅰ)求角B的大小;
(Ⅰ)求角B的大小;
(Ⅱ)若角∠BAC= ![]() ,BC邊上的中線AM的長(zhǎng)為
,BC邊上的中線AM的長(zhǎng)為 ![]() ,求△ABC的面積.
,求△ABC的面積.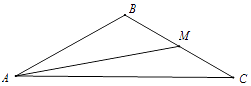
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某市為了鼓勵(lì)市民節(jié)約用電,實(shí)行“階梯式”電價(jià),將該市每戶居民的月用電量劃分為三檔,月用電量不超過(guò)200度的部分按0.5元/度收費(fèi),超過(guò)200度但不超過(guò)400度的部分按0.8元/度收費(fèi),超過(guò)400度的部分按1.0元/度收費(fèi).
(1)求某戶居民用電費(fèi)用 ![]() (單位:元)關(guān)于月用電量
(單位:元)關(guān)于月用電量 ![]() (單位:度)的函數(shù)解析式;
(單位:度)的函數(shù)解析式;
(2)為了了解居民的用電情況,通過(guò)抽樣,獲得了今年1月份100戶居民每戶的用電量,統(tǒng)計(jì)分析后得到如圖所示的頻率分布直方圖,若這100戶居民中,今年1月份用電費(fèi)用不超過(guò)260元的占80%,求 ![]() 的值;
的值;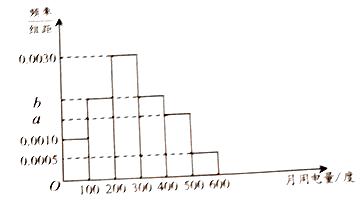
(3)在滿足(2)的條件下,估計(jì)1月份該市居民用戶平均用電費(fèi)用(同一組中的數(shù)據(jù)用該組區(qū)間的中點(diǎn)值作代表).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知在三棱柱ABC﹣A1B1C1中,B1B⊥平面ABC,∠ABC=90°,B1B=AB=2BC=4,D、E分別是B1C1 , A1A的中點(diǎn). 
(1)求證:A1D∥平面B1CE;
(2)設(shè)M是的中點(diǎn),N在棱AB上,且BN=1,P是棱AC上的動(dòng)點(diǎn),直線NP與平面MNC所成角為θ,試問(wèn):θ的正弦值存在最大值嗎?若存在,請(qǐng)求出 ![]() 的值;若不存在,請(qǐng)說(shuō)明理由.
的值;若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù) ![]() .
.
(1)求f(x)單調(diào)遞增區(qū)間;
(2)△ABC中,角A,B,C的對(duì)邊a,b,c滿足 ![]() ,求f(A)的取值范圍.
,求f(A)的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)函數(shù)f'(x)是函數(shù)f(x)(x∈R)的導(dǎo)函數(shù),f(0)=1,且 ![]() ,則4f(x)>f'(x)的解集為( )
,則4f(x)>f'(x)的解集為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】)已知函數(shù)f(x)=lnx﹣2ax,a∈R.
(1)若函數(shù)y=f(x)存在與直線2x﹣y=0平行的切線,求實(shí)數(shù)a的取值范圍;
(2)設(shè)g(x)=f(x)+ ![]() ,若g(x)有極大值點(diǎn)x1 , 求證:
,若g(x)有極大值點(diǎn)x1 , 求證: ![]() >a.
>a.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知定義域?yàn)镽的函數(shù) f (x)的導(dǎo)函數(shù)為f'(x),且滿足f'(x)﹣2f (x)>4,若 f (0)=﹣1,則不等式f(x)+2>e2x的解集為( )
A.(0,+∞)
B.(﹣1,+∞)
C.(﹣∞,0)
D.(﹣∞,﹣1)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某學(xué)校組織學(xué)生參加英語(yǔ)測(cè)試,成績(jī)的頻率分布直方圖如圖,數(shù)據(jù)的分組一次為[20,40),[40,60),[60,80),[80,100).若低于60分的人數(shù)是15人,則該班的學(xué)生人數(shù)是( ) 
A.45
B.50
C.55
D.60
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com