
【題目】已知![]() 是定義在R上的奇函數,當
是定義在R上的奇函數,當![]() 時,
時,![]() .其中
.其中![]() 且
且![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)解關于![]() 的不等式
的不等式![]() ,結果用集合或區間表示.
,結果用集合或區間表示.
科目:高中數學 來源: 題型:
【題目】已知函數![]() 為對數函數,并且它的圖象經過點
為對數函數,并且它的圖象經過點![]() ,函數
,函數![]() =
=![]() 在區間
在區間![]() 上的最小值為
上的最小值為![]() ,其中
,其中![]() .
.
(1)求函數![]() 的解析式;
的解析式;
(2)求函數![]() 的最小值
的最小值![]() 的表達式;
的表達式;
(3)是否存在實數![]() 同時滿足以下條件:①
同時滿足以下條件:①![]() ;②當
;②當![]() 的定義域為
的定義域為![]() 時,值域為
時,值域為![]() .若存在,求出
.若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,PD⊥底面ABCD,底面ABCD為正方形,PD=DC,E、F分別是AB、PB的中點 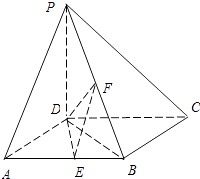
(1)求證:EF⊥CD;
(2)在平面PAD內求一點G,使GF⊥平面PCB,并證明你的結論;
(3)求DB與平面DEF所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)= ![]() sin2x﹣cos2x﹣
sin2x﹣cos2x﹣ ![]() ,(x∈R).
,(x∈R).
(1)求函數f(x)的最小值和最小正周期;
(2)設△ABC的內角A、B、C的對邊分別為a、b、c,且c= ![]() ,f(C)=0,若
,f(C)=0,若 ![]() =(1,sinA)與
=(1,sinA)與 ![]() =(2,sinB)共線,求a,b的值.
=(2,sinB)共線,求a,b的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,AD∥BC,![]() ADC=
ADC=![]() PAB=90°,BC=CD=
PAB=90°,BC=CD=![]() AD.E為棱AD的中點,異面直線PA與CD所成的角為90°.
AD.E為棱AD的中點,異面直線PA與CD所成的角為90°.

(I)在平面PAB內找一點M,使得直線CM∥平面PBE,并說明理由;
(II)若二面角P-CD-A的大小為45°,求直線PA與平面PCE所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 關于
關于![]() 軸對稱,頂點在坐標原點
軸對稱,頂點在坐標原點![]() ,直線
,直線![]() 經過拋物線
經過拋物線![]() 的焦點.
的焦點.
(1)求拋物線![]() 的標準方程;
的標準方程;
(2)若不經過坐標原點![]() 的直線
的直線![]() 與拋物線
與拋物線![]() 相交于不同的兩點
相交于不同的兩點![]() ,
, ![]() ,且滿足
,且滿足![]() ,證明直線
,證明直線![]() 過
過![]() 軸上一定點
軸上一定點![]() ,并求出點
,并求出點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,直線
,直線![]() 與平面
與平面![]() 成
成![]() 角,
角, ![]() 為
為![]() 的中點,
的中點, ![]() ,
, ![]() .
.

(Ⅰ)若![]() ,求證:平面
,求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值的取值范圍.
所成角的正弦值的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com