【題目】已知等差數列{an}的前n項和為Sn ， a1=a．當n≥2時，Sn2=3n2an+Sn﹣12 ， an≠0，n∈N* ．
（1）求a的值；
（2）設數列{cn}的前n項和為Tn ， 且cn=3n﹣1+a5 ， 求使不等式4Tn＞Sn成立的最小正整數n的值．
【答案】
（1）解：∵a1=a，當n≥2時Sn2=3n2an+Sn﹣12，
∴（a+a2）2=12a2+a2， 
=27a3﹣（a+a2）2，
∵an≠0，
∴a2=12﹣2a，a3=3+2a，
∵a1+a3=2a2，
∴2（12﹣2a）=a+3+2a，解得a=3，
經檢驗，當a=3時an=3n，Sn= 
、Sn﹣1= 
滿足Sn2=3n2an+Sn﹣12
（2）解：由（1）可知cn=3n﹣1+15，
∴Tn= 
+15n，
∵4Tn＞Sn，
∴4（ +15n）＞ ，
整理得：23n+60n﹣2＞165，即23n+60n＞167，
∵f（n）=23n+60n為增函數，且f（2）＜167、f（3）＞167，
∴滿足條件的n的最小值為3．
【解析】（1）通過在Sn2=3n2an+Sn﹣12中令n=2、3，結合a1=a計算可知a2=12﹣2a、a3=3+2a，利用a1+a3=2a2計算可知a=3，驗證其是否成立即可；（2）通過（1）可知cn=3n﹣1+15，進而利用分組求和法計算可知Tn= +15n，問題轉化為解不等式4（ +15n）＞ ，計算即得結論．
【考點精析】本題主要考查了數列的前n項和的相關知識點，需要掌握數列{an}的前n項和sn與通項an的關系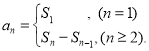
才能正確解答此題．
教材全解字詞句篇系列答案科目：高中數學 來源： 題型：
【題目】已知函數f（x）=e﹣x（lnx﹣2k）（k為常數，e=2.71828…是自然對數的底數），曲線y=f（x）在點（1，f（1））處的切線與y軸垂直．
（1）求f（x）的單調區間；
（2）設 
，對任意x＞0，證明：（x+1）g（x）＜ex+ex﹣2 ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某城市為了解游客人數的變化規律，提高旅游服務質量，收集并整理了2014年1月至2016年12月期間月接待游客量（單位：萬人）的數據，繪制了下面的折線圖．
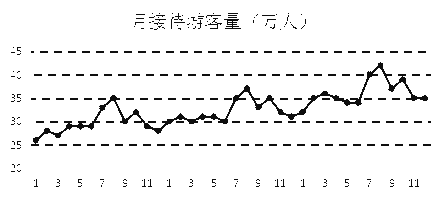
2014年 2015年 2016年
根據該折線圖，下列結論錯誤的是( )
A. 年接待游客量逐年增加
B. 月接待游客量逐月增加
C. 各年的月接待游客量高峰期大致在7，8月
D. 各年1月至6月的月接待游客量相對于7月至12月，波動性更小，變化比較平穩
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于函數
與常數
，若
恒成立，則稱
為函數
的一個“P數對”，設函數的定義域為
，且
。
（1）若是的一個“P數對”，且
，求常數的值；
（2）若（1，1）是的一個“P數對”，且在
上單調遞增，求函數在
上的最大值與最小值；
（3）若（－2，0）是的一個“P數對”，且當
時，
，求k的值及在區間
上的最大值與最小值。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數
的定義域是R，對于任意實數
，恒有
，且當
時， 
。
（1）求證： 
，且當
時，有
；
（2）判斷
在R上的單調性；
（3）設集合A＝
，B＝
，若A∩B＝
，求
的取值范圍。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，正方體ABCD﹣A′B′C′D′的棱長為1，E、F分別是棱是AA′，CC′的中點，過直線EF的平面分別與棱BB′，DD′交于M，N，設BM=x，x∈[0，1]，給出以下四種說法：
（1）平面MENF⊥平面BDD′B′；
（2）當且僅當x=
時，四邊形MENF的面積最小；
（3）四邊形MENF周長L=f（x），x∈[0，1]是單調函數；
（4）四棱錐C′﹣MENF的體積V=h（x）為常函數，以上說法中正確的為（ ）
A. （2）（3） B. （1）（3）（4） C. （1）（2）（4） D. （1）（2）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知菱形ABCD的邊長為6，∠ABD=30°，點E、F分別在邊BC、DC上，BC=2BE，CD=λCF．若 
=﹣9，則λ的值為（ ）
A.2
B.3
C.4
D.5
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
