
【題目】![]() 為何值時,方程組
為何值時,方程組![]()
(1)有一個實數解,并求出方程組的解集;
(2)有兩個不相等的實數解;
(3)沒有實數解.
【答案】(1)k=0,方程組的解為![]() ;k=1,方程組的解為
;k=1,方程組的解為![]() ;(2)k<1且k≠0;(3)k>1
;(2)k<1且k≠0;(3)k>1
【解析】
先利用代入消元法得到![]() ,
,
(1)分類討論:當k=0,易得y=2,且方程化為一次方程,解得![]() ,于是得到原方程組的一組解;當k≠0,方程為一元二次方程,若
,于是得到原方程組的一組解;當k≠0,方程為一元二次方程,若![]() ,方程有兩個相等的實數解,而對于方程組來說,只有一組實數解,然后計算出k=1,再分別求出x和y的值,得到原方程組的一組解;
,方程有兩個相等的實數解,而對于方程組來說,只有一組實數解,然后計算出k=1,再分別求出x和y的值,得到原方程組的一組解;
(2)當![]() 有兩個不相等的實數解時,方程組有兩組實數解,則k≠0,
有兩個不相等的實數解時,方程組有兩組實數解,則k≠0,![]() ,然后求出k的范圍;
,然后求出k的范圍;
(3)當![]() 沒有實數解時,方程組沒有實數解,則k≠0,
沒有實數解時,方程組沒有實數解,則k≠0,![]() ,然后求出k的范圍.
,然后求出k的范圍.
解:把![]() 代入
代入![]() 得
得![]() ,
,
整理得![]() ,
,
(1)當k=0,則![]() ,解得
,解得![]() ,
,
方程組的解為![]() ;
;
當k≠0,![]() ,解得k=1,
,解得k=1,
方程化為![]() ,解得
,解得![]() ,
,
所以![]() ,
,
所以方程組的解為![]() ;
;
(2)當k≠0,![]() ,解得k<1,
,解得k<1,
所以當k<1且k≠0時,方程組有兩個實數解;
(3)當k≠0,![]() ,解得k>1,
,解得k>1,
所以當k>1時,方程組沒有實數解.


 同步練習河南大學出版社系列答案
同步練習河南大學出版社系列答案 同步練習西南大學出版社系列答案
同步練習西南大學出版社系列答案科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
在平面直角坐標系![]() 中,已知直線
中,已知直線![]() :
:  (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() 的極坐標為
的極坐標為![]() ,直線
,直線![]() 與曲線
與曲線![]() 的交點為
的交點為![]() ,
, ![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
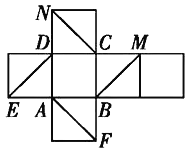
【題目】如圖所示是一個正方體的平面展開圖,在這個正方體中![]() 平面ADE;
平面ADE;![]() 平面ABF;
平面ABF;![]() 平面
平面![]() 平面AFN;
平面AFN;![]() 平面
平面![]() 平面NCF.以上四個命題中,真命題的序號是
平面NCF.以上四個命題中,真命題的序號是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
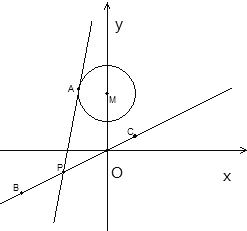
【題目】已知圓M:![]() ,設點B,C是直線l:
,設點B,C是直線l:![]() 上的兩點,它們的橫坐標分別是t,
上的兩點,它們的橫坐標分別是t,![]() ,P點的縱坐標為a且點P在線段BC上,過P點作圓M的切線PA,切點為A
,P點的縱坐標為a且點P在線段BC上,過P點作圓M的切線PA,切點為A
![]() 若
若![]() ,
,![]() ,求直線PA的方程;
,求直線PA的方程;
![]() 經過A,P,M三點的圓的圓心是D,
經過A,P,M三點的圓的圓心是D,
![]() 將
將![]() 表示成a的函數
表示成a的函數![]() ,并寫出定義域.
,并寫出定義域.
![]() 求線段DO長的最小值.
求線段DO長的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() (a>b>0)的離心率為
(a>b>0)的離心率為![]() ,短軸長為2.直線l:y=kx+m與橢圓C交于M,N兩點,又l與直線
,短軸長為2.直線l:y=kx+m與橢圓C交于M,N兩點,又l與直線![]() ,
, ![]() 分別交于A,B兩點,其中點A在第一象限,點B在第二象限,且△OAB的面積為2(O為坐標原點).
分別交于A,B兩點,其中點A在第一象限,點B在第二象限,且△OAB的面積為2(O為坐標原點).
(1)求橢圓C的方程;
(2)求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列![]() 滿足an=2an-1+2n+1(n∈N*,n≥2),
滿足an=2an-1+2n+1(n∈N*,n≥2), ![]() .
.
(1)求![]() 的值;
的值;
(2)是否存在一個實數t,使得![]() (n∈N*),且數列{
(n∈N*),且數列{![]() }為等差數列?若存在,求出實數t;若不存在,請說明理由;
}為等差數列?若存在,求出實數t;若不存在,請說明理由;
(3)求數列![]() 的前n項和
的前n項和![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
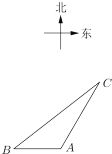
【題目】如圖,一智能掃地機器人在![]() 處發現位于它正西方向的
處發現位于它正西方向的![]() 處和北偏東30°方向上的
處和北偏東30°方向上的![]() 處分別有需要清掃的垃圾,紅外線感應測量發現機器人到
處分別有需要清掃的垃圾,紅外線感應測量發現機器人到![]() 的距離比到
的距離比到![]() 的距離少0.4米,于是選擇沿
的距離少0.4米,于是選擇沿![]() 路線清掃,已知智能掃地機器人的直線行走速度為0.2
路線清掃,已知智能掃地機器人的直線行走速度為0.2![]() ,忽略機器人吸入垃圾及在
,忽略機器人吸入垃圾及在![]() 處旋轉所用時間,10秒鐘完成了清掃任務.
處旋轉所用時間,10秒鐘完成了清掃任務.
(1)![]() 、
、![]() 兩處垃圾的距離是多少?
兩處垃圾的距離是多少?
(2)智能掃地機器人此次清掃行走路線的夾角![]() 的正弦值是多少?
的正弦值是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com