【題目】定義在
上的函數
滿足：
對任意
、
恒成立，當
時，
.
（1）求證
在
上是單調遞增函數；
（2）已知
，解關于
的不等式
；
（3）若
，且不等式
對任意
恒成立.求實數
的取值范圍.
【答案】（1）詳見解析；（2）
；（3）
.
【解析】
試題分析：（1）結合已知先構造
，可得
，利用函數的單調性的定義作差
變形可證明；（2）由f（1），及f（2）=f（1）+f（1）-2可求f（2），然后結合（I）中的函數的單調性可把已知不等式進行轉化，解二次不等式即可；（3）由f（-2）及已知可求f（-1），進而可求f（-3），由已知不等式及函數的單調性可轉化原不等式，結合恒成立與最值求解的相互轉化即可求解.
試題解析：（1）
當
時，
，所以
，所以
在
上是單調遞增函數 4分
（2）
，由
得
在上是單調遞增函數，所以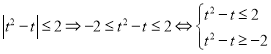
8分
（3）由
得
所以
，由
得
在上是單調遞增函數，所以
對任意
恒成立.記
只需
.對稱軸
（1）當
時，
與
矛盾.
此時
；
（2）當
時，
，又
，所以
；
（3）當
時，
又
；
綜合上述得： 14分.
科學實驗活動冊系列答案科目：高中數學 來源： 題型：
【題目】(本小題13分)已知函數f(x)＝
－
(a>0，x>0)．
(1)求證：f(x)在(0，＋∞)上是單調遞增函數；
(2)若f(x)在[
，2]上的值域是[
，2]，求a的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知{an}是等差數列，{bn}是等比數列，且b2＝3，b3＝9，a1＝b1，a14＝b4.
(1)求{an}的通項公式；
(2)設cn＝an＋bn，求數列{cn}的前n項和．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列說法：
①分類變量
與
的隨機變量
越大，說明“
與
有關系”的可信度越大.
②以模型
去擬合一組數據時，為了求出回歸方程，設
，將其變換后得到線性方程
，則
的值分別是
和0.3.
③根據具有線性相關關系的兩個變量的統計數據所得的回歸直線方程為
中， 
，
則
.正確的個數是（ ）
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】函數f(x)是R上的偶函數，且當x>0時，函數的解析式為f(x)＝
.
(1)判斷并證明f(x)在(0，＋∞)上的單調性；
(2)求當x<0時，函數的解析式．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知二次函數
的圖像經過坐標原點，其到函數為
，數列的前
項和為
，點
均在函數的圖像上．
（I）求數列
的通項公式；
（Ⅱ）設
，
是數列
的前
n項和，求使得＜
對所有都成立的最小正整數m.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知定義在區間
上的函數
，其中常數
．
（1）若函數
分別在區間
上單調，試求
的取值范圍；
（2）當
時，方程
有四個不相等的實根
．
①證明： 
；
②是否存在實數
，使得函數在區間
單調，且的取值范圍為
，若存在，求出
的取值范圍；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某種產品的廣告費用支出
（萬元）與銷售額
（萬元）之間有如下的對應數據：
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
（1）求回歸直線方程；
（2）據此估計廣告費用為12萬元時的銷售額約為多少？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
