
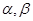 是兩個不同的平面,m,n是兩條不同的直線,給出下列命題:
是兩個不同的平面,m,n是兩條不同的直線,給出下列命題: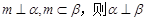 ; ②若
; ②若 ;
;  相交;
相交; 其中正確的命題是 ( )
其中正確的命題是 ( ) | A.①④ | B.②③ | C.③④ | D.①② |
 優(yōu)生樂園系列答案
優(yōu)生樂園系列答案 新編小學單元自測題系列答案
新編小學單元自測題系列答案科目:高中數(shù)學 來源:不詳 題型:單選題
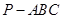 (頂點在底面的射影是底面正三角形的中心)中,
(頂點在底面的射影是底面正三角形的中心)中,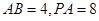 ,過
,過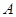 作與
作與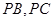 分別交于
分別交于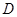 和
和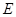 的截面,則截面
的截面,則截面
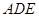 的周長的最小值是 ( )
的周長的最小值是 ( )| A.9 | B.10 | C.11 | D.12 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
 中,
中, 底面
底面 ,點
,點 ,
, 分別在棱
分別在棱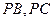 上,且
上,且 (Ⅰ)求證:
(Ⅰ)求證: 平面
平面 ;
; 為
為 的中點時,求
的中點時,求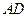 與平面
與平面 所成角的正弦值;
所成角的正弦值; 使得二面角
使得二面角 為直二面角?并說明理由.
為直二面角?并說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:填空題
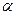 ⊥平面
⊥平面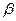 ,
,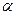 ∩
∩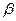 =
=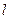 ,DA
,DA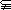
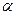 ,BC
,BC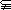
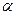 ,且DA⊥
,且DA⊥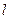 于A,BC⊥
于A,BC⊥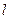 于B,AD=4,BC=8,AB=6,在平面
于B,AD=4,BC=8,AB=6,在平面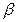 內(nèi)不在
內(nèi)不在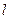 上的動點P,記PD與平面
上的動點P,記PD與平面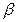 所成角為
所成角為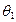 ,PC與平面
,PC與平面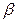 所成角為
所成角為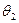 ,若
,若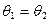 ,則△PAB的面積的最大值是 。
,則△PAB的面積的最大值是 。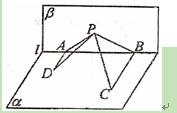
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
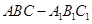 中,
中,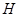 是正方形
是正方形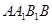 的中心,
的中心,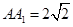 ,
,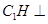 平面
平面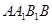 ,且
,且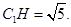
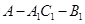 的正弦值;
的正弦值;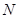 為棱
為棱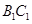 的中點,點
的中點,點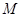 在平面
在平面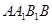 內(nèi),且
內(nèi),且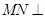 平面
平面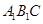 ,求線段
,求線段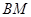 的長.
的長.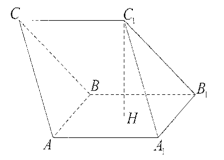
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
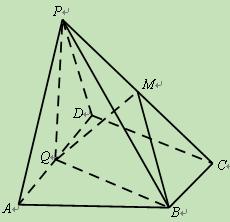
 中,底面
中,底面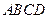 為直角梯形,
為直角梯形,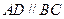 ,
,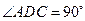 ,平面
,平面 ⊥底面
⊥底面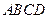 ,
,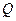 為AD的中點,
為AD的中點,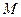 是棱
是棱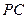 上的點,
上的點,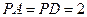 ,
,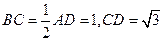 .(1)若
.(1)若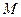 點是棱
點是棱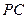 的中點,求證:
的中點,求證: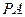
 ;(2)求證:平面
;(2)求證:平面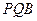 ⊥平面
⊥平面 。
。 
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com