【題目】已知函數
.
（1）當
時，求曲線
在點
處的切線方程；
（2）求函數
的單調區間；
（3）若對任意的
，都有
成立，求
的取值范圍.
【答案】（1）
（2）當
時，函數
的遞增區間為
；
當
時，函數的遞增區間為
，遞減區間為
；
（3）
【解析】
（1）
，
，
，方程易求；
（2）
，根據
的正負分類討論的單調性即可；
（3）對任意的
，使
成立，只需任意的，
，以下分、
、
三種情況討論
解：（1）
時，
，
，
∴
在點
處的切線方程為
故答案為：;
（2）
①當時，
恒成立，函數的遞增區間為
②當時，令
，解得
或
|
|
|
|
| - | + | |
| 減 | 增 |
所以函數的遞增區間為，遞減區間為
當時，恒成立，函數的遞增區間為;
當時，函數的遞增區間為，遞減區間為.
（3）對任意的，使成立，只需任意的，
①當時，在
上是增函數，
所以只需
而
所以滿足題意；
②當時，
，在
上是增函數，
所以只需
而，
所以滿足題意；
③當時，
，在
上是減函數，
上是增函數，
所以只需
即可
而
從而不滿足題意；
綜合①②③實數的取值范圍為.
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】某銷售公司擬招聘一名產品推銷員，有如下兩種工資方案：
方案一：每月底薪2000元，每銷售一件產品提成15元；
方案二：每月底薪3500元，月銷售量不超過300件，沒有提成，超過300件的部分每件提成30元．
（1）分別寫出兩種方案中推銷員的月工資
（單位：元）與月銷售產品件數
的函數關系式；
（2）從該銷售公司隨機選取一名推銷員，對他（或她）過去兩年的銷售情況進行統計，得到如下統計表：
月銷售產品件數 | 300 | 400 | 500 | 600 | 700 |
次數 | 2 | 4 | 9 | 5 | 4 |
把頻率視為概率，分別求兩種方案推銷員的月工資超過11090元的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，設
，
分別是正方體
的棱
上兩點，且
，
，其中正確的命題為（ ）
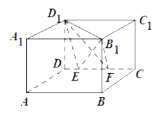
A.三棱錐
的體積為定值
B.異面直線
與
所成的角為
C.
平面
D.直線與平面所成的角為
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在2018年俄羅斯世界杯期間,莫斯科的部分餐廳經營了來自中國的小龍蝦,這些小龍蝦標有等級代碼.為得到小龍蝦等級代碼數值
與銷售單價
之間的關系,經統計得到如下數據：
等級代碼數值 | 38 | 48 | 58 | 68 | 78 | 88 |
銷售單價 | 16.8 | 18.8 | 20.8 | 22.8 | 24 | 25.8 |
（1）已知銷售單價與等級代碼數值之間存在線性相關關系,求關于的線性回歸方程(系數精確到0.1)；
（2）若莫斯科某個餐廳打算從上表的6種等級的中國小龍蝦中隨機選2種進行促銷，記被選中的2種等級代碼數值在60以下（不含60）的數量為
，求的分布列及數學期望.
參考公式：對一組數據
,
，
,其回歸直線
的斜率和截距最小二乘估計分別為：
,
.
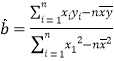參考數據：
,
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓心在直線
上的圓C經過
點，且與直線
相切.
（1）求過點P且被圓C截得的弦長等于4的直線方程；
（2）過點P作兩條相異的直線分別與圓C交于A，B，若直線PA，PB的傾斜角互補，試判斷直線AB與OP的位置關系（O為坐標原點），并證明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
