
已知空間三點(diǎn)A(0,2,3),B(-2,1,6),C(1,-1,5).
(1)求以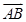 ,
,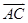 為邊的平行四邊形的面積;
為邊的平行四邊形的面積;
(2)若|a|=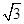 ,且a分別與
,且a分別與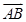 ,
,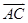 垂直,求向量a的坐標(biāo).
垂直,求向量a的坐標(biāo).
(1)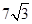 ;(2) a=(1,1,1),或a=(-1,-1,-1).
;(2) a=(1,1,1),或a=(-1,-1,-1).
解析試題分析:(1)由點(diǎn)的坐標(biāo)可得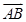 ,
,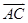 坐標(biāo),進(jìn)而求得模長(zhǎng),及夾角余弦,可利用同角間基本關(guān)系式求得夾角正弦,以
坐標(biāo),進(jìn)而求得模長(zhǎng),及夾角余弦,可利用同角間基本關(guān)系式求得夾角正弦,以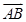 ,
,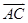 為邊的平行四邊形的面積,應(yīng)該是以
為邊的平行四邊形的面積,應(yīng)該是以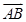 ,
,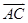 為邊的三角形面積的二倍,利用三角形面積公式可求得;(2)設(shè)
為邊的三角形面積的二倍,利用三角形面積公式可求得;(2)設(shè)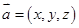 ,由兩向量垂直坐標(biāo)滿足的關(guān)系式得關(guān)于
,由兩向量垂直坐標(biāo)滿足的關(guān)系式得關(guān)于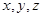 的方程組,解方程可得向量a的坐標(biāo).
的方程組,解方程可得向量a的坐標(biāo).
解:(1)由題意可得: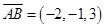 ,
,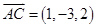 ,
,
∴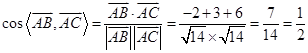 , 4分
, 4分
∴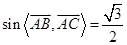 ,∴以
,∴以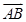 ,
,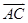 為邊的平行四邊形的面積為
為邊的平行四邊形的面積為 . 6分
. 6分
(2)設(shè)a=(x,y,z),
由題意得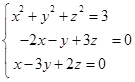 ,
,
解得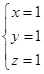 或
或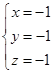 .
.
∴a=(1,1,1),或a=(-1,-1,-1) 12分
考點(diǎn):空間向量的坐標(biāo)運(yùn)算,三角形面積公式.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,四棱柱ABCD-A1B1C1D1中,側(cè)棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E為棱AA1的中點(diǎn).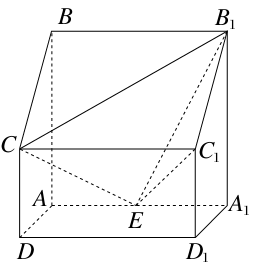
(1)證明:B1C1⊥CE;
(2)求二面角B1-CE-C1的正弦值;
(3)設(shè)點(diǎn)M在線段C1E上,且直線AM與平面ADD1A1所成角的正弦值為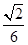 ,求線段AM的長(zhǎng).
,求線段AM的長(zhǎng).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,直三棱柱 的底面
的底面 是等腰直角三角形,
是等腰直角三角形, ,側(cè)棱
,側(cè)棱 底面
底面 ,且
,且 ,
, 是
是 的中點(diǎn),
的中點(diǎn), 是
是 上的點(diǎn).
上的點(diǎn).
(1)求異面直線 與
與 所成角
所成角 的大小(結(jié)果用反三角函數(shù)表示);
的大小(結(jié)果用反三角函數(shù)表示);
(2)若 ,求線段
,求線段 的長(zhǎng).
的長(zhǎng).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,在直三棱柱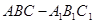 中,
中,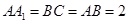 ,
,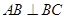 。M、N分別是AC和BB1的中點(diǎn)。
。M、N分別是AC和BB1的中點(diǎn)。
(1)求二面角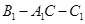 的大小。
的大小。
(2)證明:在AB上存在一個(gè)點(diǎn)Q,使得平面 ⊥平面
⊥平面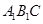 ,
,
并求出 的長(zhǎng)度。
的長(zhǎng)度。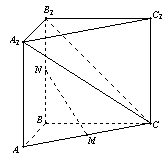
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,正方形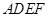 與梯形
與梯形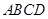 所在的平面互相垂直,
所在的平面互相垂直,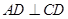 ,
, ∥
∥ ,
,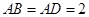 ,
,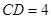 ,
,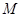 為
為 的中點(diǎn).
的中點(diǎn).
(1)求證: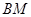 ∥平面
∥平面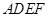 ;
;
(2)求證:平面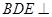 平面
平面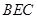 ;
;
(3)求平面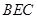 與平面
與平面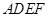 所成銳二面角的余弦值.
所成銳二面角的余弦值.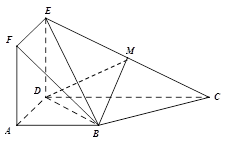
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,在△ABC中,∠ABC=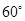 ,∠BAC
,∠BAC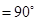 ,AD是BC上的高,沿AD把△ABD折起,使∠BDC
,AD是BC上的高,沿AD把△ABD折起,使∠BDC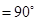 .
.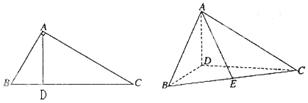
(1)證明:平面ADB⊥平面BDC;
(2)設(shè)E為BC的中點(diǎn),求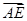 與
與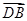 夾角的余弦值.
夾角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,在四棱錐P-ABCD中,底面ABCD是平行四邊形,且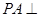 底面ABCD,
底面ABCD,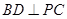 ,E是PA的中點(diǎn).
,E是PA的中點(diǎn).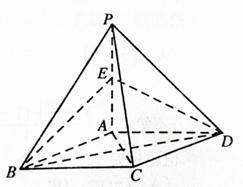
(1)求證:平面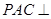 平面EBD;
平面EBD;
(2)若PA=AB=2,直線PB與平面EBD所成角的正弦值為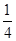 ,求四棱錐P-ABCD的體積.
,求四棱錐P-ABCD的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知四棱錐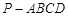 的底面為直角梯形,
的底面為直角梯形,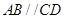 ,
,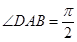 ,
,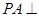 底面
底面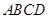 ,且
,且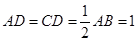 ,
,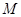 是
是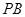 的中點(diǎn).
的中點(diǎn).
⑴求證:直線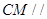 平面
平面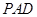 ;
;
⑵⑵若直線 與平面
與平面 所成的角為
所成的角為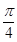 ,求二面角
,求二面角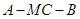 的余弦值.
的余弦值.
查看答案和解析>>