
���}Ŀ����D����ƽ��ֱ������(bi��o)ϵxOy�У��E�A![]()
![]() �����c(di��n)��
�����c(di��n)��![]() ������c(di��n)��
������c(di��n)��![]() ������c(di��n)��
������c(di��n)��![]() ��
��
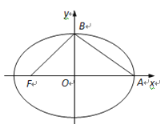
��1����֪�E�A���x���ʞ�![]() ������
������![]() ���c(di��n)�ęM����(bi��o)��
���c(di��n)�ęM����(bi��o)��![]() ����E�A�Ę�(bi��o)��(zh��n)���̣�
����E�A�Ę�(bi��o)��(zh��n)���̣�
��2����֪��![]() ��ӈA�ĈA����ֱ��
��ӈA�ĈA����ֱ��![]() �ϣ���E�A���x����
�ϣ���E�A���x����![]() ��ֵ��
��ֵ��
���𰸡���1��![]() ��2��
��2��![]()
��������
��1�����ÙE�A���x�����Լ���֪�l���D(zhu��n)�����a��b���ɵõ��E�A���̣�
��2��A��a��0����F����c��0�����������AF���д������̞飺![]() ���Ƴ�
���Ƴ�![]() ���������AB���д������̣��Ƴ�b��c��Ȼ�����E�A���x���ʼ��ɣ�
���������AB���д������̣��Ƴ�b��c��Ȼ�����E�A���x���ʼ��ɣ�
��1����?y��n)�E�A![]()
![]() ���x���ʞ�
���x���ʞ�![]() ��
��
����![]() ���t
���t![]() ��
��
��?y��n)龀��![]() ���c(di��n)�ęM����(bi��o)��
���c(di��n)�ęM����(bi��o)��![]() ��
��
����![]() ��
��
����![]() ���t
���t![]() ��
��![]() ��
��
���ԙE�A�Ę�(bi��o)��(zh��n)���̞�![]() ��
��
��2����?y��n)?/span>![]() ��
��
���Ծ���![]() ���д������̞飺
���д������̞飺![]() ��
��
����?y��n)�?/span>![]() ��ӈA�ĈA��C��ֱ��
��ӈA�ĈA��C��ֱ��![]() �ϣ�
�ϣ�
����![]() ����?y��n)?/span>
����?y��n)?/span>![]() ��
��
���Ծ���![]() ���д������̞飺
���д������̞飺![]() ��
��
��C�ھ���![]() ���д����ϣ���
���д����ϣ���![]() ��
��
�����ã�![]() ��
��
��![]() ��
��
��?y��n)?/span>![]() ������
������![]() ��
��
���ԙE�A���x����![]() ��
��


 �����u�rϵ�д�
�����u�rϵ�д� ��ӡ�Ļ��n�r�y�uϵ�д�
��ӡ�Ļ��n�r�y�uϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D��1������������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �քe��
�քe��![]() �ăɂ����ȷ��c(di��n)�����ѵ���������̓��
�ăɂ����ȷ��c(di��n)�����ѵ���������̓��![]() ��
��![]() ����ʹ���c(di��n)
����ʹ���c(di��n)![]() ���c(di��n)
���c(di��n)![]() �غϣ�ӛ���c(di��n)
�غϣ�ӛ���c(di��n)![]() �� ��D��2����
�� ��D��2����

��1�����C��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����ƽ��![]() �cƽ��
�cƽ��![]() �����J����ǵ�����ֵ��
�����J����ǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��)P�ǙE�A![]() ��һ�c(di��n)��M��N�քe�ǃɈA(x��4)2��y2��1��(x��4)2��y2��1�ϵ��c(di��n)���t|PM|��|PN|����Сֵ�����ֵ�քe�� �� ��
��һ�c(di��n)��M��N�քe�ǃɈA(x��4)2��y2��1��(x��4)2��y2��1�ϵ��c(di��n)���t|PM|��|PN|����Сֵ�����ֵ�քe�� �� ��
A. 9,12 B. 8,11 C. 10,12 D. 8,12
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
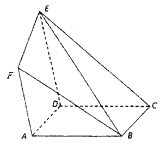
���}Ŀ����D���ڶ����w![]() �У�����
�У�����![]() ����Σ���(c��)��
�������(c��)��![]() ������
������![]() ��
��![]() .
.
��1�����C��![]() ��
��
��2�����C��![]() ƽ��
ƽ��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪��(sh��)��![]() ��ǰ
��ǰ![]() 헺͞�
헺͞�![]() .��(sh��)��
.��(sh��)��![]() �M��
�M��![]() ��
��![]() .
.
��1����![]() ����
����![]() ����������(sh��)
����������(sh��)![]() ��ֵ��
��ֵ��
��2������(sh��)��![]() ��
��![]() ���ǵȲ(sh��)�У���
���ǵȲ(sh��)�У���![]() ��ȡֵ������
��ȡֵ������
��3������(sh��)��![]() �ǵȱȔ�(sh��)�У����Ȟ�
�ǵȱȔ�(sh��)�У����Ȟ�![]() ����
����![]() ���Ƿ����������(sh��)
���Ƿ����������(sh��)![]() ��ʹ
��ʹ![]() ��
��![]() ��
��![]() �ɵȲ(sh��)�У������ڣ����һ��
�ɵȲ(sh��)�У������ڣ����һ��![]() ��ֵ���������ڣ�Ո�f������.
��ֵ���������ڣ�Ո�f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij���������˹�(ji��)�s������늣�Ӌ���ڱ���ԇ�о���������늶��~���������_��һ���������������(bi��o)��(zh��n)a������������^a�IJ��ְ�ƽ�r���M(f��i)������a�IJ��ְ��h�r���M(f��i)![]() ��ˣ������{(di��o)����100���������ƽ�������
��ˣ������{(di��o)����100���������ƽ�������![]() ��λ����
�����![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ֽM���l�ʷֲ�ֱ���D��D��ʾ��
�ֽM���l�ʷֲ�ֱ���D��D��ʾ��
![]() ����(j��)�l�ʷֲ�ֱ���D�Ĕ�(sh��)��(j��)����ֱ���D��x��ֵ����Ӌԓ��ÿ��������ƽ�������
����(j��)�l�ʷֲ�ֱ���D�Ĕ�(sh��)��(j��)����ֱ���D��x��ֵ����Ӌԓ��ÿ��������ƽ�������![]() ��ֵ��
��ֵ��
![]() ���l�ʹ�Ӌ���ʣ�����
���l�ʹ�Ӌ���ʣ�����![]() �ĽY(ji��)�������O(sh��)ԓ��ÿ��������ƽ�������X�������B(t��i)�ֲ�
�ĽY(ji��)�������O(sh��)ԓ��ÿ��������ƽ�������X�������B(t��i)�ֲ�![]()
![]() ��Ӌԓ�о�����ƽ�����������
��Ӌԓ�о�����ƽ�����������![]() ��֮�g�ĸ��ʣ�
��֮�g�ĸ��ʣ�
![]() ����
����![]() �ĽY(ji��)Փ����ԓ�����о������S�C(j��)��ȡ3����ӛ��ƽ�����������
�ĽY(ji��)Փ����ԓ�����о������S�C(j��)��ȡ3����ӛ��ƽ�����������![]() ��֮�g�đ���(sh��)��
��֮�g�đ���(sh��)��![]() ����
����![]() �ķֲ��м���(sh��)�W(xu��)����
�ķֲ��м���(sh��)�W(xu��)����![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����1����֪�ɂ�׃���������P(gu��n)�������������P(gu��n)��Խ��(qi��ng)���t���P(gu��n)ϵ��(sh��)�Ľ^��ֵԽ�ӽ���1.
��2�����Իؚwֱ�����^�c(di��n)![]() ��
��
��3�����ڷ��׃��A�cB���S�C(j��)׃��![]() ��
��![]() Խ���f����A�cB���P(gu��n)ϵ���Ŀ��Ŷ�Խ��.
Խ���f����A�cB���P(gu��n)ϵ���Ŀ��Ŷ�Խ��.
��4���ڿ̮��ؚwģ�͵ĔM��Ч���r������ƽ����ԽС�����P(gu��n)ָ��(sh��)![]() ��ֵԽ���f���M�ϵ�Ч��Խ��.
��ֵԽ���f���M�ϵ�Ч��Խ��.
��5������(j��)��С���˷���һ�M�ӱ��c(di��n)![]() ����õĻؚw������
����õĻؚw������![]() �������еĽ��׃��
�������еĽ��׃��![]() ,
,![]() ��ֵһ���c
��ֵһ���c![]() ���`��.
���`��.
�������}���_����̖��____________.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D���ڵ��������ε������F![]() �У�
��![]() ��
��![]() ��
��![]() ���c(di��n)
���c(di��n)![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��
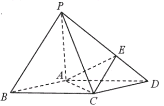
��1���C����![]() ��
��![]() ��
��
��2������![]() ���Ƿ����һ�c(di��n)
���Ƿ����һ�c(di��n)![]() ��ʹ�����F
��ʹ�����F![]() ���������F���C����ĽY(ji��)Փ��
���������F���C����ĽY(ji��)Փ��
��3������![]() ���⣬
���⣬![]() �c
�c![]() ����Ķ����
����Ķ����![]() �Ĵ�С��
�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
����������(sh��)![]() ��
��![]() �rȡ�ØOֵ����(sh��)��(sh��)
�rȡ�ØOֵ����(sh��)��(sh��)![]() ��ֵ��
��ֵ��
����(d��ng)![]() �r����
�r����![]() ���c(di��n)����(sh��).
���c(di��n)����(sh��).
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com