Question

【題目】已知某幾何體的三視圖和直觀圖如圖所示,其正視圖為矩形,左視圖為等腰直角三角形,俯視圖為直角梯形.

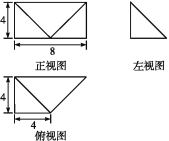
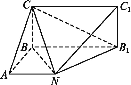
(1)證明:平面BCN⊥平面C1NB1;

(2)求二面角C-NB1-C1的余弦值.

Answer 1

【答案】（1）見解析；（2）

【解析】

(1)建立空間直角坐標系，根據坐標運算，求得直線與平面的垂直，進而判斷平面與平面的垂直。

(2)根據空間直角坐標系，求出兩個平面的法向量，進而利用兩個平面的法向量求出兩個平面的二面角大小。

(1)證明∵該幾何體的正視圖為矩形,左視圖為等腰直角三角形,俯視圖為直角梯形,∴BA,BC,BB1兩兩垂直.

以分別作為x,y,z軸的正方向,建立如圖所示的空間直角坐標系,

則B(0,0,0),N(4,4,0),B1(0,8,0),C1(0,8,4),C(0,0,4),=-16+16+0=0,=0,

∴NB⊥NB1,NB⊥B1C1.

又NB1與B1C1相交于B1,∴NB⊥平面C1NB1.

又NB平面BCN.

∴平面BCN⊥平面C1NB1.

(2)解設n=(x,y,z)是平面NCB1的一個法向量,=(4,4,-4),=(4,-4,0),

則

取x=1,得n=(1,1,2).

由(1)知=(4,4,0)是平面C1B1N的一個法向量,

cos<n,>=.

故二面角C-NB1-C1的余弦值為.