
(本小題滿分10分)
函數f(x)=Asin(ωx-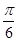 )+1(A>0,ω>0)的最大值為3,其圖象相鄰兩條對稱軸之間的距離為
)+1(A>0,ω>0)的最大值為3,其圖象相鄰兩條對稱軸之間的距離為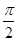 .
.
(1)求函數f(x)的解析式;
(2)設α∈(0,2π),f(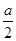 )=2,求α的值.
)=2,求α的值.
(1)f(x)=2sin(2x- )+1.(2)α=
)+1.(2)α= ,或α=π.
,或α=π.
【解析】
試題分析:(1)∵函數f(x)的最大值為3,∴A+1=3,即A=2,
∵函數圖象的相鄰兩條對稱軸之間的距離為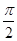 ,
,
∴最小正周期T=π,∴ω=2.
故函數f(x)的解析式為f(x)=2sin(2x- )+1.
)+1.
(2)f(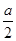 )=2sin(α-
)=2sin(α- )+1=2,即sin(α-
)+1=2,即sin(α- )=
)=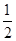 .
.
∵0<α<2π,∴- <α-
<α- <
<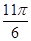 ,
,
∴α- =
= ,或α-
,或α- =
=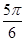 ,
,
故α= ,或α=π.
,或α=π.
考點:函數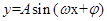 的性質;三角函數求值。
的性質;三角函數求值。
點評:本題為基礎題型,我們在做題時要認真、仔細,確保得滿分。求函數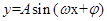 的解析式,我們一般根據最值求A,根據周期
的解析式,我們一般根據最值求A,根據周期 求
求 ,找點代入求
,找點代入求 ,
,


 智趣暑假溫故知新系列答案
智趣暑假溫故知新系列答案 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案科目:高中數學 來源: 題型:
 (選做題)本題包括A、B、C、D四小題,請選定其中兩題,并在答題卡指定區域內作答,若多做,則按作答的前兩題評分,解答時應寫出文字說明、證明過程或演算步驟.
(選做題)本題包括A、B、C、D四小題,請選定其中兩題,并在答題卡指定區域內作答,若多做,則按作答的前兩題評分,解答時應寫出文字說明、證明過程或演算步驟.
|
|
| 1 |
| 2a |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
查看答案和解析>>
科目:高中數學 來源: 題型:
 本題包括(1)、(2)、(3)、(4)四小題,請選定其中兩題,并在答題卡指定區域內答,
本題包括(1)、(2)、(3)、(4)四小題,請選定其中兩題,并在答題卡指定區域內答,
|
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com