(本小題10分)求經過兩直線3x + 4y – 5 = 0與2x – 3y + 8 = 0的交點M，且與直線L1：2x + y + 5 = 0平行的直線L2的方程，并求L1與L2間的距離。
科目：高中數學 來源：2011年山東省濟南外國語學校高一入學檢測數學試卷 題型：解答題
（（本小題12分）
經市場調查，某超市的一種小商品在過去的近20天內的銷售量(件)與價格(元)均為時間t(天)
的函數，且銷售量近似滿足g(t)=80-2t，價格近似滿足f(t)=20-
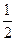|t-10|.
(1)試寫出該種商品的日銷售額y與時間t(0≤t≤20)的函數表達式；
(2)求該種商品的日銷售額y的最大值與最小值.
查看答案和解析>>
科目：高中數學 來源：2010-2011學年廣東省高考猜押題卷文科數學（二）解析版 題型：解答題
（本小題滿分12分）
新能源汽車是指除汽油、柴油發動機之外所有其它能源汽車.包括燃料電池汽車、混合動力汽車、氫能源動力汽車和太陽能汽車等.其廢氣排放量比較低.為了配合我國“節能減排”戰略，某汽車廠決定轉型生產新能源汽車中的燃料電池汽車、混合動力和氫能源動力三類轎車,每類轎車均有標準型和豪華型兩種型號,某月的產量如下表(單位:輛):
|
|
燃料電池轎車 |
混合動力轎車 |
氫能源動力轎車 |
|
標準型 |
100 |
200 |
|
|
豪華型 |
200 |
300 |
500 |
按類型分層抽樣的方法在這個月生產的轎車中抽取100輛,其中有燃料電池轎車20輛.
(I) 求
的值.
(II) 用分層抽樣的方法在氫能源動力轎車中抽取一個容量為7的樣本.將該樣本看成一個總體,從中任取2輛,求至少有1輛標準型轎車的概率;
(Ⅲ) 用隨機抽樣的方法從混合動力標準型轎車中抽取10輛,經檢測它們的得分如下:
9.3, 8.7, 9.1, 9.5, 8.8, 9.4, 9.0, 8.2，9.6, 8.4.
把這10輛轎車的得分看作一個總體,從中任取一個數,求該數與樣本平均數之差的絕對值不超過0.4的概率.
查看答案和解析>>
科目：高中數學 來源：2011年山東省高一入學檢測數學試卷 題型：解答題
（（本小題12分）
經市場調查，某超市的一種小商品在過去的近20天內的銷售量(件)與價格(元)均為時間t(天)的函數，且銷售量近似滿足g(t)=80-2t，價格近似滿足f(t)=20-
|t-10|.
(1)試寫出該種商品的日銷售額y與時間t(0≤t≤20)的函數表達式；
(2)求該種商品的日銷售額y的最大值與最小值.
查看答案和解析>>
科目：高中數學 來源：2013屆黑龍江省高二上學期期末考試理科數學 題型：解答題
（本小題滿分12分）
經統計，某大型商場一個結算窗口每天排隊結算的人數及相應的概率如下：
|
排隊人數 |
0~5 |
6~10 |
11~15 |
16~20 |
21~25 |
25人以上 |
|
概 率 |
0.1 |
0.15 |
0.25 |
0.25 |
0.2 |
0.05 |
（1）求每天不超過20人排隊結算的概率；
（2）一周7天中，若有3天以上（含3天）出現超過15人排隊結算的概率大于0.75，商場就需要增加結算窗口，試問該商場是否需要產加結算窗口？
查看答案和解析>>
科目：高中數學 來源：2010年山東省高二下學期期末考試數學卷 題型：解答題
(本小題滿分12分）
某工廠生產一種精密儀器， 產品是否合格需先后經過兩道相互獨立的工序檢查，且當第一道工序檢查合格后才能進入到第二道工序，經長期檢測發現，該儀器第一道工序檢查合格的概率為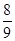
，第二道工序檢查合格的概率為
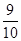，已知該廠每月生產3臺這種儀器.
（1）求生產一臺合格儀器的概率;
（2）用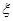
表示每月生產合格儀器的臺數，求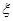的分布列和數學期望;
（3）若生產一臺合格儀器可盈利10萬元，不合格要虧損3萬元，求該廠每月的期望盈利額.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
解得
……………………4分
………………………………6分
…………………………10分
