【題目】已知拋物線
上在第一象限內(nèi)的點H(1，t)到焦點F的距離為2．
(1)若
，過點M，H的直線與該拋物線相交于另一點N，求
的值；
(2)設A、B是拋物線E上分別位于x軸兩側的兩個動點，且
(其中O為坐標原點)．
①求證：直線AB必過定點，并求出該定點Q的坐標；
②過點Q作AB的垂線與該拋物線交于G、D兩點，求四邊形AGBD面積的最小值．
【答案】(1) 
(2) ①見證明； ②最小值88
【解析】
（1）根據(jù)
點的坐標和拋物線的定義，求得
的值，進而求得拋物線
的方程以及點的坐標，由此求得直線
的方程，聯(lián)立直線的方程和拋物線的方程，求得
點的橫坐標，利用拋物線的定義求得
的值.（2）①設出直線
的方程，與拋物線方程聯(lián)立，寫出韋達定理，利用向量數(shù)量積的坐標運算，化簡
，由此證得直線過定點. ②利用①的結論求得
,由此求得四邊形
面積
的表達式，換元后利用二次函數(shù)的單調(diào)性來求得四邊形面積的最小值.
解：（1）∵點
，∴
，解得
，
故拋物線E的方程為：
，
所以當
時
，
∴直線的方程為
，聯(lián)立可得，
，
.
（2）①證明：設直線
，
，
聯(lián)立拋物線方程可得
，
，
由得：
，解得
或
（舍去），
即
，所以直線過定點
；
②由①得
同理得，
.
則四邊形面積
.
令
，則
是關于
的增函數(shù)，
故當
時，
.當且僅當
時取到最小值88.
期末寶典單元檢測分類復習卷系列答案科目：高中數(shù)學 來源： 題型：
【題目】已知橢圓
的離心率為
，點
在橢圓
上.
(1)求橢圓的方程；
(2)若不過原點
的直線
與橢圓相交于
兩點，與直線
相交于點
，且是線段
的中點，求
面積的最大值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】為征求個人所得稅法修改建議，某機構對當?shù)鼐用竦脑率杖胝{(diào)查了10000人，并根據(jù)所得數(shù)據(jù)畫了樣本的頻率分布直方圖(每個分組包括左端點，不包括右端點，如第一組表示收入在[1000,1500))．
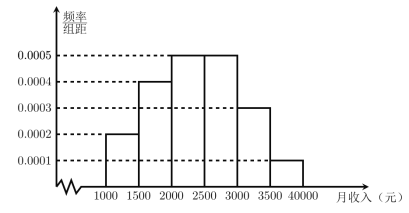
(1)求居民月收入在
的頻率；
(2)根據(jù)頻率分布直方圖估算樣本數(shù)據(jù)的中位數(shù)；
(3)為了分析居民的收入與年齡、職業(yè)等方面的關系，必須按月收入再從這10000人中用分層抽樣方法抽出100人作進一步分析，則月收入在
的這段應抽多少人？
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】邗江中學高二年級某班某小組共10人，利用寒假參加義工活動，已知參加義工活動次數(shù)為1，2，3的人數(shù)分別為3，3，4．現(xiàn)從這10人中選出2人作為該組代表參加座談會．
（1）記“選出2人參加義工活動的次數(shù)之和為4”為事件
，求事件發(fā)生的概率；
（2）設
為選出2人參加義工活動次數(shù)之差的絕對值，求隨機變量的分布列和數(shù)學期望．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在平面直角坐標系xOy中，過點P(0，1)且互相垂直的兩條直線分別與圓O：
交于點A，B，與圓M：(x﹣2)2＋(y﹣1)2＝1交于點C，D．
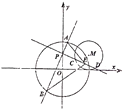
（1）若AB＝
，求CD的長；
（2）若CD中點為E，求△ABE面積的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，內(nèi)接于圓
的正方形
邊長為1，圓
內(nèi)切于正方形，正方形
內(nèi)接于圓，···，正方形
內(nèi)接于圓
，圓
內(nèi)切于正方形，正方形
內(nèi)接于圓，由此無窮個步驟進行下去記圓
的面積記作
，記正方形
的面積記作
．
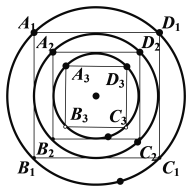
（1）求
的值
（2）記
的所有項和為
，
的所有項和為
，求
的值．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
