【題目】如圖所示為一正方體的平面展開圖，在這個正方體中，有下列四個命題：
①AF⊥GC；
②BD與GC成異面直線且夾角為60；
③BD∥MN；
④BG與平面ABCD所成的角為45.
其中正確的個數(shù)是( )
A. 1 B. 2 C. 3 D. 4
科目：高中數(shù)學 來源： 題型：
【題目】如圖，已知橢圓
： 
的離心率為
，上、下頂點分別為
、
，點
在橢圓上，且異于點
、
，直線
、
與直線
： 
分別交于點
、
，且
面積的最大值為
.
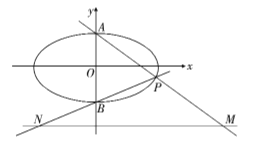
（1）求橢圓
的標準方程；
（2）求線段
的長的最小值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
(m,n∈R)在x=1處取得極值2.
(1)求f(x)的解析式；
(2)k為何值時，方程f(x)-k=0只有1個根
(3)設函數(shù)g(x)=x2-2ax+a，若對于任意x1∈R，總存在x2∈[-1,0]，使得g(x2)≤f(x1)，求a的取值范圍
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】有一矩形硬紙板材料（厚度忽略不計），一邊
長為6分米，另一邊足夠長．現(xiàn)從中截取矩形
（如圖甲所示），再剪去圖中陰影部分，用剩下的部分恰好能折卷成一個底面是弓形的柱體包裝盒（如圖乙所示，重疊部分忽略不計），其中
是以
為圓心、
的扇形，且弧
,
分別與邊
, 
相切于點
, 
．
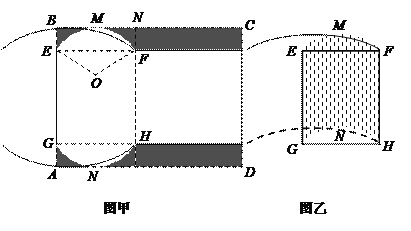
（1）當
長為1分米時，求折卷成的包裝盒的容積；
（2）當
的長是多少分米時，折卷成的包裝盒的容積最大？
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】將圓
上每個點的橫坐標變?yōu)樵瓉淼?/span>4倍，縱坐標變?yōu)樵瓉淼?/span>3倍，得曲線
，以坐標原點為極點， 
軸的非負軸分別交于
半軸為極軸建立極坐標系，直線
的極坐標方程為： 
，且直線
在直角坐標系中與
軸分別交于
兩點.
（1）寫出曲線
的參數(shù)方程，直線
的普通方程；
（2）問在曲線
上是否存在點
，使得
的面積
，若存在，求出點
的坐標，若不存在，請說明理由.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在直角坐標系xOy中，直線l經過點P(2,0)，其傾斜角為，在以原點O為極點，x軸非負半軸為極軸的極坐標系中（取相同的長度單位），曲線C的極坐標方程為
．
（Ⅰ）若直線l與曲線C有公共點，求傾斜角的取值范圍；
（Ⅱ）設M(x,y)為曲線C上任意一點，求
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
是定義在
上的偶函數(shù).當
時， 
.
(1) 求曲線
在點
處的切線方程；
(2) 若關于
的不等式
恒成立,求實數(shù)
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知坐標平面上動點
與兩個定點
， 
，且
.
（1）求點
的軌跡方程，并說明軌跡是什么圖形；
（2）記（1）中軌跡為
，過點
的直線
被
所截得的線段長度為8，求直線
的方程.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某花店每天以每枝5元的價格從農場購進若干枝玫瑰花，然后以每枝10元的價格出售，如果當天賣不完，剩下的玫瑰花作垃圾處理.
（Ⅰ）若花店一天購進17枝玫瑰花，求當天的利潤
（單位：元）關于當天需求量
（單位：枝， 
）的函數(shù)解析式.
（Ⅱ）花店記錄了100天玫瑰花的日需求量（單位：枝），整理得下表：
以100天記錄的各需求量的頻率作為各需求量發(fā)生的概率.
（1）若花店一天購進17枝玫瑰花， 
表示當天的利潤（單位：元），求
的分布列及數(shù)學期望；
（2）若花店計劃一天購進16枝或17枝玫瑰花，以利潤角度看，你認為應購進16枝好還是17枝好？請說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
